题目内容
数列{an}满足an+1+(-1)nan=2n-1,且a1=2,Sn是an的前n和.
(1)求a2,a3,a4,a5,a6,a7,a8;
(2)求an;
(3)求Sn.
(1)求a2,a3,a4,a5,a6,a7,a8;
(2)求an;
(3)求Sn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由{an}满足an+1+(-1)nan=2n-1,且a1=2,利用递推思想能求出a2,a3,a4,a5,a6,a7,a8.
(2)由(1)猜想:a4k-3=2,a4k-2=8k-5,a4k-1=0,a4k=8k-3,再利用数学归纳法证明.
(3)当n=4k时,Sn=2k+(4k2-k)+0+(4k2+k);当n=4k-1时,Sn=S4k-1=S4k-a4k;当n=4k-2时,Sn=S4k-2=S4k-a4k-a4k-1;当n=4k-3时,Sn=S4k-3=S4k-a4k-a4k-1-a4k-2,由此利用分类讨论思想能求出Sn.
(2)由(1)猜想:a4k-3=2,a4k-2=8k-5,a4k-1=0,a4k=8k-3,再利用数学归纳法证明.
(3)当n=4k时,Sn=2k+(4k2-k)+0+(4k2+k);当n=4k-1时,Sn=S4k-1=S4k-a4k;当n=4k-2时,Sn=S4k-2=S4k-a4k-a4k-1;当n=4k-3时,Sn=S4k-3=S4k-a4k-a4k-1-a4k-2,由此利用分类讨论思想能求出Sn.
解答:
解:(1)∵数列{an}满足an+1+(-1)nan=2n-1,且a1=2,
∴a2-2=1,解得a2=3,
a3+3=3,解得a3=0,
a4-0=5,解得a4=5,
a5+5=7,解得a5=2,
a6-2=9,解得a6=11,
a7+11=11,解得a7=0,
a8-0=13,解得a8=13.…(2分)
(2)由(1)猜想:a4k-3=2,a4k-2=8k-5,a4k-1=0,a4k=8k-3.…(3分)
用数学归纳法证明:
①n=1,2,3,4时已经验证.
②n=4k(k≥1)时,猜想如上,
则a4k+1+(-1)4ka4k=2(4k)-1,即a4k+1=8k-1-(8k-3)=2,
a4k+2+(-1)4k+1a4k+1=2(4k+1)-1,
即a4k+2=2(4k+1)-1+2=8(k+1)-5,…(5分)
a4k+3+(-1)4k+2a4k+2=2(4k+2)-1,
即a4k+3=2(4k+2)-1-(8k+3),
a4k+4+(-1)4k+3a4k+3=2(4k+3)-1,
即a4k+4=2(4k+3)-1-0=8(k+1)-3.
由①、②可知,当n=4k+1时,猜想成立.…(7分)
从而an=
.…(8分)
(3)当n=4k时,Sn=2k+(4k2-k)+0+(4k2+k)
=8k2+2k=
,…(10分)
当n=4k-1时,Sn=S4k-1=S4k-a4k
=8k2+2k-(8k-3)
=8k2-6k+3
=
,…(11分)
当n=4k-2时,Sn=S4k-2=S4k-a4k-a4k-1
=8k2+2k-(8k-3)
=8k2-6k+3
=
,…(13分)
当n=4k-3时,Sn=S4k-3=S4k-a4k-a4k-1-a4k-2
=8k2+2k-(8k-3)-(8k-5)
=8k2-14k+8
=
.…(15分)
综合上述,Sn=
.…(16分)
∴a2-2=1,解得a2=3,
a3+3=3,解得a3=0,
a4-0=5,解得a4=5,
a5+5=7,解得a5=2,
a6-2=9,解得a6=11,
a7+11=11,解得a7=0,
a8-0=13,解得a8=13.…(2分)
(2)由(1)猜想:a4k-3=2,a4k-2=8k-5,a4k-1=0,a4k=8k-3.…(3分)
用数学归纳法证明:
①n=1,2,3,4时已经验证.
②n=4k(k≥1)时,猜想如上,
则a4k+1+(-1)4ka4k=2(4k)-1,即a4k+1=8k-1-(8k-3)=2,
a4k+2+(-1)4k+1a4k+1=2(4k+1)-1,
即a4k+2=2(4k+1)-1+2=8(k+1)-5,…(5分)
a4k+3+(-1)4k+2a4k+2=2(4k+2)-1,
即a4k+3=2(4k+2)-1-(8k+3),
a4k+4+(-1)4k+3a4k+3=2(4k+3)-1,
即a4k+4=2(4k+3)-1-0=8(k+1)-3.
由①、②可知,当n=4k+1时,猜想成立.…(7分)
从而an=
|
(3)当n=4k时,Sn=2k+(4k2-k)+0+(4k2+k)
=8k2+2k=
| n2+n |
| 2 |
当n=4k-1时,Sn=S4k-1=S4k-a4k
=8k2+2k-(8k-3)
=8k2-6k+3
=
| n2-n+4 |
| 2 |
当n=4k-2时,Sn=S4k-2=S4k-a4k-a4k-1
=8k2+2k-(8k-3)
=8k2-6k+3
=
| n2+n+4 |
| 2 |
当n=4k-3时,Sn=S4k-3=S4k-a4k-a4k-1-a4k-2
=8k2+2k-(8k-3)-(8k-5)
=8k2-14k+8
=
| n2-n+4 |
| 2 |
综合上述,Sn=
|
点评:本题考查数列的通项公式和前n项和公式的应用,是基础题,解题时要认真审题,注意数学归纳法和分类讨论思想的合理运用.

练习册系列答案
相关题目
已知|
|=3,|
|=4且向量
与
的夹角是
,则向量
在
方向上的投影是( )
| a |
| b |
| a |
| b |
| π |
| 6 |
| a |
| b |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
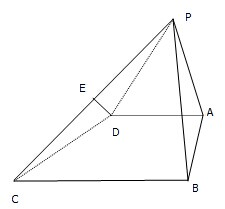 如图所示,在四棱锥P-ABCD中,△PAB为正三角形,且面PAB⊥面ABCD,四边形ABCD为直角梯形,且AD∥BC,∠BCD=
如图所示,在四棱锥P-ABCD中,△PAB为正三角形,且面PAB⊥面ABCD,四边形ABCD为直角梯形,且AD∥BC,∠BCD=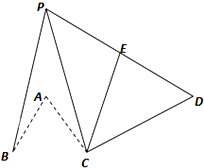 在如图所示的四棱锥P-ABCD中,已知PA⊥平面ABCD,AD∥BC,∠BAD=90°,PA=AB=BC=1,AD=2,E为PD的中点.
在如图所示的四棱锥P-ABCD中,已知PA⊥平面ABCD,AD∥BC,∠BAD=90°,PA=AB=BC=1,AD=2,E为PD的中点.
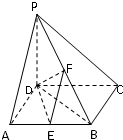 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,PD=DC,E、F分别为AB、PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,PD=DC,E、F分别为AB、PB的中点.