题目内容
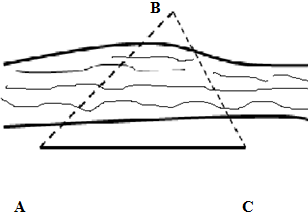如图，在一次测量活动中，要测量河两岸B、C两点间的距离，测量者在河的一侧，测得AC=24m，∠BAC=45°，∠ACB=75°，求B、C两点间的距离．考点：解三角形的实际应用
专题：解三角形
分析：先求得∠ABC，进而根据正弦定理求得BC．
解答：
解：由三角形的内角和定理，有
∠ABC=180°-∠BAC-∠ACB=60°，
又由正弦定理有：
=
，
∴BC=
=8
（m）
所以B、C两点间的距离为8
m．
∠ABC=180°-∠BAC-∠ACB=60°，
又由正弦定理有：
| BC |
| sin∠BAC |
| AC |
| sin∠ABC |
∴BC=
| AC•sin∠BAC |
| sin∠ABC |
| 6 |
所以B、C两点间的距离为8
| 6 |
点评：本题主要考查了运用正弦定理解决三角形实际问题．考查了学生运用三角函数解决实际问题的能力．
练习册系列答案
相关题目
若△ABC 的三边长分别为a，b，c，面积为s．则△ABC的内切圆半径 r=
；类似的，若四面体ABCD的四个面的面积分别为s1，s2，s3，s4，体积为V，则四面体ABCD的内切球半径r为（ ）
| 2s |
| a+b+c |
A、
| ||
B、
| ||
C、
| ||
D、
|
某英语学习小组共12名同学进行英语听力测试，随机抽取6名同学的测试成绩（单位：分），用茎叶图记录如下，其中茎为十位数，叶为个位数．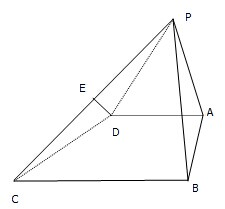
如图所示，在四棱锥P-ABCD中，△PAB为正三角形，且面PAB⊥面ABCD，四边形ABCD为直角梯形，且AD∥BC，∠BCD=