题目内容
17.已知函数f(x)=$\frac{lnx}{x}$,g(x)=x2-(a+b)x+ab,其中a<b,a,b∈R+.(1)?x∈R+,f(x)≤kx恒成立,求实数k的取值范围;
(2)若g(e)>0,比较ab与ba的大小.
分析 (1)问题等价于lnx-kx2≤0恒成立,令h(x)=lnx-kx2,(x>0),求出h(x)的导数,通过讨论k的符号,得到h(x)的单调性,求出h(x)的最大值,从而求出k的范围即可;
(2)先求出b>a>e,再利用函数f(x)的单调性和对数的运算性质即可得到结论.
解答 解:(1))?x∈R+,f(x)≤kx恒成立,
等价于lnx-kx2≤0恒成立,
令h(x)=lnx-kx2,(x>0),
则h′(x)=$\frac{1}{x}$-2kx=$\frac{1-2{kx}^{2}}{x}$,
显然k≤0,h′(x)>0,h(x)递增,不合题意,
k>0时,令h′(x)>0,解得:x<$\sqrt{\frac{1}{2k}}$,令h′(x)<0,解得:x>$\sqrt{\frac{1}{2k}}$,
∴h(x)在(0,$\sqrt{\frac{1}{2k}}$)递增,在($\sqrt{\frac{1}{2k}}$,+∞)递减,
∴h(x)max=h($\sqrt{\frac{1}{2k}}$)=ln$\sqrt{\frac{1}{2k}}$-k•$\frac{1}{2k}$≤0,
解得:k≥$\frac{1}{2e}$;
(2)g(x)=x2-(a+b)x+ab=(x-a)(x-b),其中a<b,a,b∈R+,
由g(e)=(e-a)(e-b)>0,得:b>a>e,或a<b<e,
由函数f(x)=$\frac{lnx}{x}$,
则f′(x)=$\frac{1-lnx}{{x}^{2}}$,当x>e时,f′(x)<0,0<x<e时,f′(x)>0,
即函数f(x)在(0,e)递增,在(e,+∞)递减,
①若e<a<b,
∴$\frac{lna}{a}$>$\frac{lnb}{b}$,即blna>alnb,
即lnab>lnba,
则ab>ba;
②若a<b<e,
∴$\frac{lna}{a}$<$\frac{lnb}{b}$,即blna<alnb,
即lnab<lnba,
则ab<ba.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,转化思想;本题还考查了指数幂的大小比较,根据已知条件,利用函数的单调性是解决本题的关键,综合性较强有一定的难度,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $({0,\frac{4}{27}})$ | B. | $({0,\frac{4}{27}}]$ | C. | $({\frac{4}{27},\frac{2}{3}})$ | D. | $({\frac{4}{27},\frac{2}{3}}]$ |
| A. | 2$\sqrt{5}$ | B. | $\sqrt{19}$+$\sqrt{2}$ | C. | 4+$\sqrt{5}$ | D. | 3$\sqrt{5}$ |
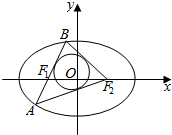 如图,设椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左右焦点分别为F1,F2,过焦点F1的直线交椭圆于A(x1,y1),B(x2,y2)两点,若△ABF2的内切圆的面积为π,则|y1-y2|=3.
如图,设椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左右焦点分别为F1,F2,过焦点F1的直线交椭圆于A(x1,y1),B(x2,y2)两点,若△ABF2的内切圆的面积为π,则|y1-y2|=3.