题目内容
7.若关于x的方程|x4-x3|=ax在R上存在4个不同的实根,则实数a的取值范围为( )| A. | $({0,\frac{4}{27}})$ | B. | $({0,\frac{4}{27}}]$ | C. | $({\frac{4}{27},\frac{2}{3}})$ | D. | $({\frac{4}{27},\frac{2}{3}}]$ |
分析 根据方程和函数的关系转化为函数,利用参数分离法,构造函数,求函数的导数,研究函数的单调性和极值,利用数形结合进行求解即可.
解答 解:当x=0时,0=0,∴0为方程的一个根.
当x>0时,方程|x4-x3|=ax等价为a=|x3-x2|,
令f(x)=x3-x2,f′(x)=3x2-2x,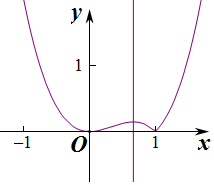
由f′(x)<0得0<x<$\frac{2}{3}$,由f′(x)>0得x<0或x>$\frac{2}{3}$,
∴f(x)在$({0,\frac{2}{3}})$上递减,在$({-∞,0}),({\frac{2}{3},+∞})$上递增,又f(1)=0,
∴当x=$\frac{2}{3}$时,函数f(x)取得极小值f($\frac{2}{3}$)=-$\frac{4}{27}$,则|f(x)|取得极大值|f($\frac{2}{3}$)|=$\frac{4}{27}$,
∴设$g(x)=\frac{{|{{x^4}-{x^3}}|}}{x}=\left\{\begin{array}{l}|{f(x)}|,x>0\\-|{f(x)}|,x<0\end{array}\right.$的图象如下图所示,
则由题可知当直线y=a与g(x)的图象有3个交点时0<a<$\frac{4}{27}$,
此时方程|x4-x3|=ax在R上存在4个不同的实根,
故$a∈({0,\frac{4}{27}})$.
故选:A.
点评 本题主要考查函数与方程的应用,利用数形结合以及导数法是解决本题的关键.综合性较强,运算量较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.定义在R上的函数f(x)、g(x)满足:对任意的实数x都有f(x)=f(|x|),g(-x)+g(x)=0,当x>0时.f′(x)>0,g′(x)<0,则当x<0时,有( )
| A. | f′(x)>0,g′(x)>0 | B. | f′(x)>0,g′(x)<0 | C. | f′(x)<0,g′(x)<0 | D. | f′(x)<0,g′(x)>0 |
12.在区间[-3,3]上随机取一个数x,使得|x+1|-|x-2|≥1成立的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
16.复数(2+i)(1-i)等于( )
| A. | 1-i | B. | 2-i | C. | 3+i | D. | 3-i |
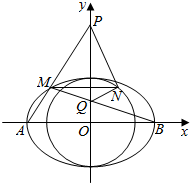 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})过点({2,\sqrt{2}})$,其焦点在⊙O:x2+y2=4上,A,B是椭圆的左右顶点.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})过点({2,\sqrt{2}})$,其焦点在⊙O:x2+y2=4上,A,B是椭圆的左右顶点.