题目内容
6.已知⊙O:x2+y2=4和⊙C:x2+y2-12x+27=0.(1)判断⊙O和⊙C的位置关系;
(2)过⊙C的圆心C作⊙O的切线l,求切线l的方程.
分析 (1)圆的方程化为标准方程,求出圆心与半径,即可判断⊙O和⊙C的位置关系;
(2)过显然,切线斜率存在,设为k,利用点到直线的距离公式求出k,即可求切线l的方程.
解答 解:(1)由题意知,O(0,0),r1=2; …(1分)
∵⊙C:x2+y2-12y+27=0,∴x2+(x-6)2=9,圆心C(0,6),r2=3…3分
∵|OC|=6>r1+r2…(5分)
∴⊙O与⊙C相离. …(6分)
(2)显然,切线斜率存在,设为k.…(7分)
∴切线l:y=kx+6,即kx-y+6=0.
∴$\frac{6}{{\sqrt{{k^2}+{{(-1)}^2}}}}=2$ …(10分)
解得k=±2$\sqrt{2}$,∴切线方程为$y=±2\sqrt{2}x+6$…(12分)
点评 本题考查圆与圆的位置关系,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
16.复数(2+i)(1-i)等于( )
| A. | 1-i | B. | 2-i | C. | 3+i | D. | 3-i |
16.设集合S={x|x>1},T={x||x-1|≤2},则(∁RS)∪T( )
| A. | (-∞,3] | B. | [-1,1] | C. | [-1,3] | D. | [-1,+∞) |
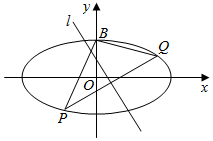 已知中心在原点O,焦点在x轴上的椭圆的一个顶点为B(0,1),B到焦点的距离为2.
已知中心在原点O,焦点在x轴上的椭圆的一个顶点为B(0,1),B到焦点的距离为2.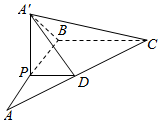 如图,在△ABC中,∠B=$\frac{π}{2}$,AB=BC=2,P为AB上一动点,PD∥BC交AC于点D,现将△PDA沿PD翻折至△PDA′,使平面PDA′⊥平面PBCD.
如图,在△ABC中,∠B=$\frac{π}{2}$,AB=BC=2,P为AB上一动点,PD∥BC交AC于点D,现将△PDA沿PD翻折至△PDA′,使平面PDA′⊥平面PBCD.