题目内容
12.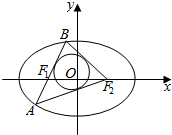 如图,设椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左右焦点分别为F1,F2,过焦点F1的直线交椭圆于A(x1,y1),B(x2,y2)两点,若△ABF2的内切圆的面积为π,则|y1-y2|=3.
如图,设椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左右焦点分别为F1,F2,过焦点F1的直线交椭圆于A(x1,y1),B(x2,y2)两点,若△ABF2的内切圆的面积为π,则|y1-y2|=3.
分析 由已知△ABF2内切圆半径r=1.,从而求出△ABF2,再由ABF2面积=$\frac{1}{2}$|y1-y2|×2c,能求出|y1-y2|.
解答 解:∵椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左右焦点分别为F1,F2, a=3,b=$\sqrt{5}$,c=2,
a=3,b=$\sqrt{5}$,c=2,
过焦点F1的直线交椭圆于A(x1,y1),B(x2,y2)两点,△ABF2的内切圆的面积为π,
∴△ABF2内切圆半径r=1.
△ABF2面积S=$\frac{1}{2}$×1×(AB+AF2+BF2)=2a=6,
∴ABF2面积S=$\frac{1}{2}$|y1-y2|×2c=.$\frac{1}{2}$|y1-y2|×2×2=6,
∴|y1-y2|=3.
故答案为:3.
点评 本题考查两点纵坐标之差的绝对值的求法,是中档题,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
相关题目
20.已知直线y=kx+1,当k变化时,此直线被椭圆$\frac{{x}^{2}}{4}$+y2=1截得的最大弦长是( )
| A. | 4 | B. | $\frac{4\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
 一果农种植了1000棵果树,为估计其产量,从中随机选取20棵果树的产量(单位:kg)作为样本数据,得到如图所示的频率分布直方图.已知样本中产量在区间(45,50]上的果树棵数为8,.
一果农种植了1000棵果树,为估计其产量,从中随机选取20棵果树的产量(单位:kg)作为样本数据,得到如图所示的频率分布直方图.已知样本中产量在区间(45,50]上的果树棵数为8,.