题目内容
8.椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),A为长轴的一个顶点,B为短轴的一个顶点,F为右焦点,且AB⊥BF,则椭圆M的离心率e为$\frac{\sqrt{5}-1}{2}$.分析 由已知得AB2+BF2=AF2,从而a2+b2+a2=(a+c)2,由此能求出椭圆M的离心率e.
解答  解:如图,∵椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
解:如图,∵椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
A为长轴的一个顶点,B为短轴的一个顶点,
F为右焦点,且AB⊥BF,
∴AB2+BF2=AF2,
∴a2+b2+a2=(a+c)2,
把b2=a2-c2,e=$\frac{c}{a}$代入整理,得:
e2+e-1=0,
解得e=$\frac{\sqrt{5}-1}{2}$或e=$\frac{-1-\sqrt{5}}{2}$(舍),
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 本题考查椭圆的离心率的求法,是中档题,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
16.复数(2+i)(1-i)等于( )
| A. | 1-i | B. | 2-i | C. | 3+i | D. | 3-i |
20.已知直线y=kx+1,当k变化时,此直线被椭圆$\frac{{x}^{2}}{4}$+y2=1截得的最大弦长是( )
| A. | 4 | B. | $\frac{4\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
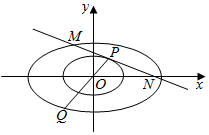 如图,已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,点A(0,$\sqrt{3}$)和点P都在椭圆C1上,椭圆C2方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=4.
如图,已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,点A(0,$\sqrt{3}$)和点P都在椭圆C1上,椭圆C2方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=4.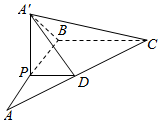 如图,在△ABC中,∠B=$\frac{π}{2}$,AB=BC=2,P为AB上一动点,PD∥BC交AC于点D,现将△PDA沿PD翻折至△PDA′,使平面PDA′⊥平面PBCD.
如图,在△ABC中,∠B=$\frac{π}{2}$,AB=BC=2,P为AB上一动点,PD∥BC交AC于点D,现将△PDA沿PD翻折至△PDA′,使平面PDA′⊥平面PBCD.