题目内容
2.在棱长为2的正方体ABCD-A1B1C1D1中,E为A1B1的中点,则异面直线D1E和BC1间的距离是( )| A. | $\frac{2\sqrt{6}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{6}}{3}$ |
分析 以D为原点,DA,DC,DD1所在直线分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出异面直线D1E和BC1间的距离.
解答 解: 以D为原点,DA,DC,DD1所在直线分别为x,y,z轴,
以D为原点,DA,DC,DD1所在直线分别为x,y,z轴,
建立空间直角坐标系,
D1(0,0,2),E(2,1,2),B(2,2,0),C1(0,2,2),
$\overrightarrow{{D}_{1}E}$=(2,1,0),$\overrightarrow{B{C}_{1}}$=(-2,0,2),$\overrightarrow{BE}$=(0,-1,2),
设$\overrightarrow{{D}_{1}E}$,$\overrightarrow{B{C}_{1}}$的公共法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{{D}_{1}E}=2x+y=0}\\{\overrightarrow{n}•\overrightarrow{B{C}_{1}}=-2x+2z=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,-2,1),
∴异面直线D1E和BC1间的距离:
d=$\frac{|\overrightarrow{n}•\overrightarrow{BE}|}{|\overrightarrow{n}|}$=$\frac{4}{\sqrt{6}}=\frac{2\sqrt{6}}{3}$.
故选:A.
点评 本题考查异面直线间的距离的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
18.下列命题是真命题的是( )
| A. | ?φ∈R,函数f(x)=sin(2x+φ)都不是偶函数 | |
| B. | ?α,β∈R,使cos(α+β)=cosα+cosβ | |
| C. | 向量$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(-1,0),则$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为2 | |
| D. | “|x|≤1”是“x≤1”的既不充分又不必要条件 |
19.已知等比数列{an}为递增数列,若a1>0,且2(an+2-an)=3an+1,则数列{an}的公比q=( )
| A. | 2或$\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | -2 |
16.锐角△ABC中,内角A,B,C的对边分别为a,b,c,且满足(a-b)(sinA+sinB)=(c-b)sinC,若$a=\sqrt{3}$,则b2+c2的取值范围是( )
| A. | (5,6] | B. | (3,5) | C. | (3,6] | D. | [5,6] |
11.复数$\frac{(1+i)(3+4i)}{i}$等于( )
| A. | 7+i | B. | 7-i | C. | 7+7i | D. | -7+7i |
12.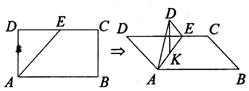 如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
 如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{{\sqrt{6}+\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{6}+\sqrt{2}}}{2}$ |