题目内容
2.已知指数函数f(x)=ax(a>0且a≠1)的图象过点P(2,4),则在(0,10]内任取一个实数x,使得f(x)>16的概率为$\frac{3}{5}$.分析 设函数f(x)=ax,a>0 且a≠1,把点(2,4),求得a的值,可得函数的解析式,进而结合几何概型可得到答案.
解答 解:指数函数f(x)=ax(a>0且a≠1)的图象过点P(2,4),代入可得 a2=4,
解得a=2,
∴f(x)=2x.
又∵x∈(0,10],
若f(x)>16,则x∈(4,10],
∴f(x)>16的概率P=$\frac{10-4}{10-0}$=$\frac{3}{5}$,
故答案为$\frac{3}{5}$.
点评 本题主要考查用待定系数法求函数的解析式,几何概型,是函数和概率的综合应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.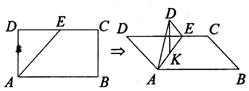 如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
 如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{{\sqrt{6}+\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{6}+\sqrt{2}}}{2}$ |
13.抛物线y2=2x的准线方程是( )
| A. | x=$\frac{1}{2}$ | B. | x=1 | C. | x=-$\frac{1}{2}$ | D. | x=-1 |
14.若中心在原点,焦点在y轴上的双曲线离心率为$\sqrt{3}$,则此双曲线的渐近线方程为( )
| A. | y=±x | B. | $y=±\frac{{\sqrt{2}}}{2}x$ | C. | $y=±\sqrt{2}x$ | D. | $y=±\frac{1}{2}x$ |
12.已知$\overrightarrow a=({1,cosa}),\overrightarrow b=({sina,1})$,若$\overrightarrow a⊥\overrightarrow b$,则sin2α=( )
| A. | $-\frac{1}{2}$ | B. | -1 | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |