题目内容
已知函数y=ax2+bx+c的图象如图所示，则下列结论正确的是（ ）
| A、a＞0，c＞0 |
| B、a＜0，c＜0 |
| C、a＜0，c＞0 |
| D、a＞0，c＜0 |
考点：二次函数的性质
专题：函数的性质及应用
分析：根据图象的开口方向即可知道a＞0，该二次函数的零点一正一负，即一元二次方程ax2+bx+c=0有两个互异实数根，所以
＜0，所以c＜0．
| c |
| a |
解答：
解：由二次函数图象可得：
；
∴a＞0，c＜0．
故选D．
|
∴a＞0，c＜0．
故选D．
点评：考查二次函数图象的开口方向和二次项系数的关系，二次函数函数与x轴交点和对应一元二次方程实数根的关系以及韦达定理．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
已知锐角α满足cosα-sinα=-
，则
等于（ ）
| ||
| 5 |
| 2sinαcosα+2sin2α |
| 1-tanα |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
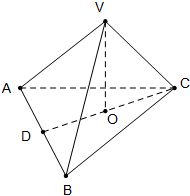如图，在三棱锥V-ABC中，VO⊥平面ABC，O∈CD，VA=VB=