题目内容
已知函数f(x)=ax2-2x+1.
(1)当x∈[1,2]时,f(x)>0恒成立,求实数a的取值范围;
(2)若函数g(x)=|f(x)|(a≥0)在[1,2]上是增函数,求实数a的取值范围.
(1)当x∈[1,2]时,f(x)>0恒成立,求实数a的取值范围;
(2)若函数g(x)=|f(x)|(a≥0)在[1,2]上是增函数,求实数a的取值范围.
考点:函数恒成立问题
专题:函数的性质及应用
分析:(1)将f(x)>0分离参变量转化为最值问题.
(2)对a进行分类讨论即可.
(2)对a进行分类讨论即可.
解答:
解:(1)当x∈[1,2]时,ax2-2x+1>0恒成立,可以化为:a>-
+
=-(
-1)2+1 恒成立,又-(
-1)2+1在x∈[1,2]上的最大值为1,所以a>1.
(2)当a=0时,g(x)=2|2x-1|在[1,2]时上是增函数;
当a>0时,g(x)=|a(x-
)2+1-
|
①若1-
≥0,
≤1,即a≥1时,g(x)=|a(x-
)2+1-
|=a(x-
)2+1-
在[1,2]上是增函数;
②若1-
<0,即0<a<1时,设方程f(x)=0的两根为x1 x2且x1>x2,此时g(x)
在[x1,
]和[x2,+∞)上是增函数,
1°若[1,2]⊆[x1,
],则
,解得0<a≤
;
2°若[1,2]⊆[x2,+∞)则
得a>1,无解;
综上所述0≤a≤
或a≥1.
| 1 |
| x2 |
| 2 |
| x |
| 1 |
| x |
| 1 |
| x |
(2)当a=0时,g(x)=2|2x-1|在[1,2]时上是增函数;
当a>0时,g(x)=|a(x-
| 1 |
| a |
| 1 |
| a |
①若1-
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
②若1-
| 1 |
| a |
在[x1,
| 1 |
| a |
1°若[1,2]⊆[x1,
| 1 |
| a |
|
| 1 |
| 2 |
2°若[1,2]⊆[x2,+∞)则
|
综上所述0≤a≤
| 1 |
| 2 |
点评:本题以求范围为载体讨论了函数的恒成立与函数的单调性问题,属于中档题,难度较大.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
已知各项均为正数的等差数列{an}的前20项和为100,那么a2•a19的最大值是( )
| A、50 | ||
| B、25 | ||
| C、100 | ||
D、4
|
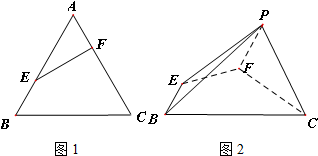 在图1等边三角形ABC中,AB=2,E是线段AB上的点(除点A外),过点E作EF⊥AC于点F,将△AEF 沿EF折起到△PEF(点A与点P重合,如图2),使得∠PFC=
在图1等边三角形ABC中,AB=2,E是线段AB上的点(除点A外),过点E作EF⊥AC于点F,将△AEF 沿EF折起到△PEF(点A与点P重合,如图2),使得∠PFC=