题目内容
4. 如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,$AB=\sqrt{2},AF=1$,M在线段EF上.
如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,$AB=\sqrt{2},AF=1$,M在线段EF上.(1)若M是线段EF的中点,证明:平面AMD⊥平面BDF;
(2)命题“若M为线段EF的中点,则平面ADM⊥平面BDF”的逆命题是否成立?若成立,给出证明,否则请举出反例.
分析 (1)推导出BD⊥AC,从而BD⊥平面MA,设AC∩BD=O,连结FO,推导出MA⊥FO,MA⊥FO,由此能证明平面AMD⊥平面BDF.
(2)设AC∩BD=O,OF∩AM=G,连结OF、DG,过F作FH⊥DG于H,推导出AM⊥平面BDF,从而AM⊥OF,∠AMF=∠AFG=$\frac{π}{4}$,进而MF=AF=1,M为EF的中点,从而命题“若M为线段EF的中点,则平面ADM⊥平面BDF”的逆命题是真命题.
解答 证明:(1)在正方形ABCD中,BD⊥AC,BD?平面ABCD,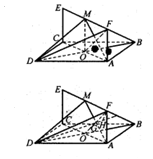
又∵正方形ABCD和矩形ACEF所在平面互相垂直,且交线是AC,
∴BD⊥平面MA,
设AC∩BD=O,连结FO,
∵AB=$\sqrt{2}$,AF=1,M是线段EF的中点,
∴四边形AFMO是正方形,∴MA⊥FO,
∵FO∩BD=O,又MA⊥BD,
∵FO∩BD=O,∴MA⊥平面BDF.
∵MA?平面AMD,∴平面AMD⊥平面BDF.
解:(2)命题“若M为线段EF的中点,则平面ADM⊥平面BDF”的逆命题是真命题.
证明如下:
设AC∩BD=O,OF∩AM=G,连结OF、DG,
过F作FH⊥DG于H,
∴平面ADM∩平面BDF=DG,
∵平面ADM⊥平面BDF,FH?平面BDF,
∴FH⊥平面ADM,
∴FH⊥AM,即AM⊥FH,
∵AM⊥BD,BD、FH相交,∴AM⊥平面BDF,∴AM⊥OF,
∴∠AMF=∠AFG,
∵OA=AF=1,∴$∠AFG=\frac{π}{4}$,$∠AMF=\frac{π}{4}$,
∴MF=AF=1,∵正方形ABCD中,AB=$\sqrt{2}$,
∴EF=AC=$\sqrt{2+2}=2$,∴M为EF的中点.
点评 本题考查线面垂直的证明,考查原命题的逆否命题是否成立的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、数形结合思想,是中档题.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
附表
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3,841 | 6.635 | 10.828 |
| A. | 2 | B. | -2 | C. | $±\frac{1}{2}$ | D. | ±2 |
| A. | x1,x2,…,xn的平均数 | B. | x1,x2,…,xn的标准差 | ||
| C. | x1,x2,…,xn的最大值 | D. | x1,x2,…,xn的中位数 |
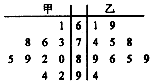 甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如图所示的茎叶图.
甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如图所示的茎叶图.