题目内容
 若程序框图如图所示,视x为自变量,y为函数值,可得函数y=f(x)的解析式,则f(x)>f(2)的解集为( )
若程序框图如图所示,视x为自变量,y为函数值,可得函数y=f(x)的解析式,则f(x)>f(2)的解集为( )| A、(2,+∞) |
| B、(4,5] |
| C、(-∞,-2]4 |
| D、(-∞,-2)∪(3,5,5] |
考点:程序框图
专题:不等式的解法及应用,算法和程序框图
分析:由程序框图可确定此程序框图的算法功能为求分段函数的值,根据判断框的条件列出每段的解析式,从而得到函数y=f(x)的解析式,在各段中令y>f(2)=4,从而求出f(x)>f(2)的解集.
解答:
解:当x≤2时,y=x2;
当2<x≤5时,y=2x-3;
当x>5时,y=
;
∴y关于x的函数解析式为y=
;
∴f(2)=4.
∵f(x)>f(2)=4,
当x≤2时,x2>4,解得x<-2;
当2<x≤5时,2x-3>4,可解得
<x≤5;
当x>5时,
>4,无解.
综上可得:f(x)>f(2)的解集为(-∞,-2)∪(3.5,5].
故选:D.
当2<x≤5时,y=2x-3;
当x>5时,y=
| 1 |
| x |
∴y关于x的函数解析式为y=
|
∴f(2)=4.
∵f(x)>f(2)=4,
当x≤2时,x2>4,解得x<-2;
当2<x≤5时,2x-3>4,可解得
| 7 |
| 2 |
当x>5时,
| 1 |
| x |
综上可得:f(x)>f(2)的解集为(-∞,-2)∪(3.5,5].
故选:D.
点评:本题主要考察了算法和程序框图,不等式的解法及应用,属于基本知识的考查.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
函数f(x)=4x-x4的图象大致是( )
A、 |
B、 |
C、 |
D、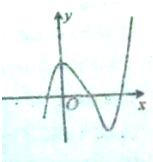 |
双曲线x2-2y2=1的离心率是( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
已知正项等比数列{an}中,3a1,
a3,2a2成等差数列,则
=( )
| 1 |
| 2 |
| a2011+a2012 |
| a2009+a2010 |
| A、3或-1 | B、9或1 | C、1 | D、9 |
已知椭圆
+
=1上一点P到两焦点距离的乘积为m,当m取得最大值时,点P的坐标是( )
| x2 |
| 9 |
| y2 |
| 16 |
| A、(3,0)和(-3,0) |
| B、(0,3)和(0,-3) |
| C、(4,0)和(-4,0) |
| D、(0,4)和(0,-4) |

