题目内容
17.已知全集U={2,4,6,8,10},集合A,B满足∁U(A∪B)={8,10},A∩∁UB={2},则集合B=( )| A. | {4,6} | B. | {4} | C. | {6} | D. | Φ |
分析 由A与B并集的补集得到元素8,10不属于B,再由A与B补集的交集得到元素2不属于B,即可得出B,
解答 解:∵全集U={2,4,6,8,10},
∁U(A∪B)={8,10},
∴A∪B={2,4,6},
又∵A∩{∁UB}={2},
∴B={4,6}.
故选:A.
点评 此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
12.已知全集U=R,集合A={x|x<-1或x>4),B={x|-2≤x≤3),那么阴影部分表示的集合为( )
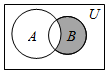

| A. | {x|-2≤x<4} | B. | {x|x≤3或x≥4} | C. | {x|-2≤x≤一1} | D. | {x|-1≤x≤3} |
2.2015年“双十一”当天,甲、乙两大电商进行了打折促销活动,某公司分别调查了当天在甲、乙电商购物的1000名消费者的消费金额,得到了消费金额的频数分布表如下:
甲电商:
乙电商:
(Ⅰ)根据频数分布表,完成下列频率分布直方图,并根据频率分布直方图比较消费者在甲、乙电商消费金额的中位数的大小以及方差的大小(其中方差大小给出判断即可,不必说明理由);
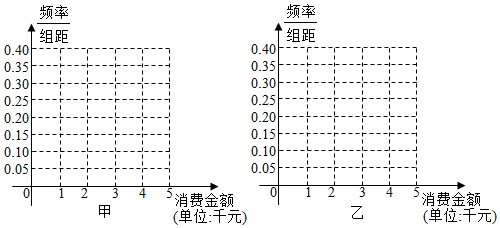
(Ⅱ)运用分层抽样分别从甲、乙1000名消费者中各自抽出20人放在一起,在抽出的40人中,从消费金额不小于4千元的人中任取2人,求这2人恰好是来自不同电商消费者的概率.
甲电商:
| 消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
| 频数 | 50 | 200 | 350 | 300 | 100 |
| 消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
| 频数 | 250 | 300 | 150 | 100 | 200 |

(Ⅱ)运用分层抽样分别从甲、乙1000名消费者中各自抽出20人放在一起,在抽出的40人中,从消费金额不小于4千元的人中任取2人,求这2人恰好是来自不同电商消费者的概率.
9.若函数f(x)=ln(x+$\sqrt{a+{x}^{2}}$)为奇函数,则a=( )
| A. | -1 | B. | 0 | C. | 1 | D. | -1或1 |
6.某产品在某零售摊位的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如表所示:
由此表可得回归直线方程$\widehat{y}$=-3.2x+$\widehat{a}$,据此模型预测零售价为5元时,每天的销售量为( )
| X | 11 | 10.5 | 10 | 9.5 | 9 |
| y | 5 | 6 | 8 | 10 | 11 |
| A. | 23个 | B. | 24个 | C. | 25个 | D. | 26个 |
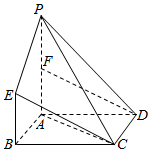 如图,矩形ABCD中,BC=2,AB=1,PA⊥平面ABCD,BE∥PA,BE=$\frac{1}{2}$PA,F为PA的中点.
如图,矩形ABCD中,BC=2,AB=1,PA⊥平面ABCD,BE∥PA,BE=$\frac{1}{2}$PA,F为PA的中点.