题目内容
7．若集合A={x||x-3|＜2}，集合B={x|$\frac{x-4}{x}≥0$}，则A∩B=[4，5）．分析 分别求出A与B中不等式的解集确定出A与B，找出两集合的交集即可．
解答 解：由A中不等式变形得：-2＜x-3＜2，
解得：1＜x＜5，即A=（1，5），
由B中不等式变形得：x（x-4）≥0，且x≠0，
解得：x＜0或x≥4，即B=（-∞，0）∪[4，+∞），
则A∩B=[4，5），
故答案为：[4，5）
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
17．已知全集U={2，4，6，8，10}，集合A，B满足∁U（A∪B）={8，10}，A∩∁UB={2}，则集合B=（ ）
| A． | {4，6} | B． | {4} | C． | {6} | D． | Φ |
已知抛物线C：x2=4y，F为抛物线焦点，圆E：x2+（y+1）2=1，斜率为k（k＞0）的直线l与抛物线C和圆E都相切，切点分别为P和Q，直线PF和PQ分别交x轴于点M，N．
12．
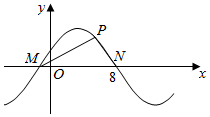如图所示，M，N是函数y=2sin（ωx+ϕ）（ω＞0）图象与x轴的交点，点P在M，N之间的图象上运动，当△MPN面积最大时，PM⊥PN，则ω=（ ）
如图所示，M，N是函数y=2sin（ωx+ϕ）（ω＞0）图象与x轴的交点，点P在M，N之间的图象上运动，当△MPN面积最大时，PM⊥PN，则ω=（ ）| A． | $\frac{π}{4}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{2}$ | D． | 8 |
17．三角形的一个内角为60°是这个三角形三内角成等差数列的（ ）条件．
| A． | 充分不必要 | B． | 必要不充分 | ||
| C． | 充要 | D． | 既不充分也不必要 |