题目内容
8.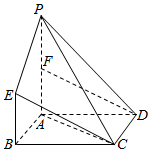 如图,矩形ABCD中,BC=2,AB=1,PA⊥平面ABCD,BE∥PA,BE=$\frac{1}{2}$PA,F为PA的中点.
如图,矩形ABCD中,BC=2,AB=1,PA⊥平面ABCD,BE∥PA,BE=$\frac{1}{2}$PA,F为PA的中点.(1)求证:PC∥平面BDF.
(2)记四棱锥C-PABE的体积为V1,三棱锥P-ACD的体积为V2,求$\frac{V_1}{V_2}$的值.
分析 (1)取AC中点O,连结OF,由中位线定理得OF∥PC,故PC∥平面BDF;
(2)设BE=a,求出V1,V2.
解答 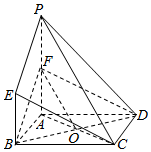 (1)证明:连结BF,连接BD交AC与点O,连OF,
(1)证明:连结BF,连接BD交AC与点O,连OF,
依题得O为AC中点,又F为PA的中点,
所以OF为△PAC中位线,所以OF∥PC
因为OF?平面BDF,PC?平面BDF
所以PC∥平面BDF.
(2)解:设BE=a,则PA=2BE=2a,
∴V1=$\frac{1}{3}{S}_{梯形ABEP}•BC$=$\frac{1}{3}×\frac{1}{2}$(a+2a)×1×2=a.
V2=$\frac{1}{3}{S}_{△PAD}•CD$=$\frac{1}{3}×\frac{1}{2}×2×2a×1$=$\frac{2a}{3}$.
∴$\frac{V_1}{V_2}=\frac{3}{2}$.
点评 本题考查了线面平行的判定,棱锥的体积计算,属于基础题.

练习册系列答案
相关题目
19.已知全集U=R,集合A={x|-2≤x<0},B={x|2x-1<$\frac{1}{4}$},则A∩B=( )
| A. | (-∞,-2)∪(-1,+∞) | B. | (-∞,-2)∪[-1,+∞) | C. | [-2,-1) | D. | (-2,+∞) |
20.已知变量x,y满足$\left\{{\begin{array}{l}{x-2y+4≥0}\\{x≤2}\\{x+y-2≥0}\end{array}}\right.$,则z=x2+y2+2x+2y的取值范围是( )
| A. | [8,23] | B. | [8,25] | C. | [6,23] | D. | [6,25] |
17.已知全集U={2,4,6,8,10},集合A,B满足∁U(A∪B)={8,10},A∩∁UB={2},则集合B=( )
| A. | {4,6} | B. | {4} | C. | {6} | D. | Φ |
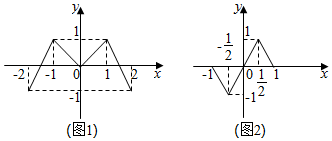 已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,若f(y0)=0且y0=g(x0),则x0的值为-1,0,或1.
已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,若f(y0)=0且y0=g(x0),则x0的值为-1,0,或1.