题目内容
3.已知定义在R上的奇函数f(x)满足f(x)=x2-2x-3(x>0).(Ⅰ) 若函数g(x)=|f(x)|-a有4个零点,求实数a的取值范围;
(Ⅱ) 求|f(x+1)|≤4的解集.
分析 (Ⅰ)利用f(x)是定义在R上的奇函数,求出函数的解析式,画出函数y=f(x)与y=|f(x)|的图象,利用函数g(x)=|f(x)|-a有4个零点,转化为函数y=|f(x)|与函数y=a的图象有4个交点.推出实数a的取值范围即可.
(Ⅱ)令f(x)=4得,$x=2\sqrt{2}+1$或-1,利用函数f(x)是定义在R上的奇函数,结合图象,求解即可.
解答 (本小题满分12分)
解:(Ⅰ)因为f(x)是定义在R上的奇函数,且f(x)=x2-2x-3(x>0),
则$f(x)=\left\{\begin{array}{l}{x^2}-2x-3,(x>0)\\ 0,(x=0)\\-{x^2}-2x+3,(x<0)\end{array}\right.$.…(2分)
从而可得函数y=f(x)与y=|f(x)|的图象分别如下图所示.…(4分)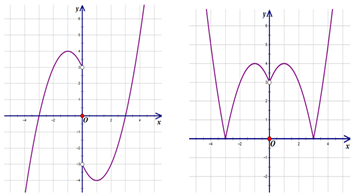
因为函数g(x)=|f(x)|-a有4个零点,
则题设可等价转化为函数y=|f(x)|与函数y=a的图象有4个交点.…(5分)
由右上图可知,a=4或0<a≤3,…(6分)
即:当a=4或0<a≤3时,函数g(x)=|f(x)|-a有4个零点.…(7分)
(Ⅱ)令f(x)=4得,$x=2\sqrt{2}+1$或-1,…(8分)
因为f(x)是定义在R上的奇函数,当f(x)=-4时,解得$x=-2\sqrt{2}-1$或1…(9分)
结合左上图可知,$|{f(x+1)}|≤4?-2\sqrt{2}-1≤x+1≤2\sqrt{2}+1$,…(10分)
即:$-2\sqrt{2}-2≤x≤2\sqrt{2}$.…(11分)
所以所求解集为$[-2\sqrt{2}-2,2\sqrt{2}]$. …(12分)
点评 本题考查函数与方程的应用,函数的图象的应用,考查数形结合思想以及转化思想的应用,考查计算能力.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案| A. | 62 | B. | 64 | C. | 126 | D. | 128 |
| A. | $\frac{58}{5}$ | B. | $\frac{23}{2}$ | C. | $\sqrt{33}$ | D. | $2\sqrt{33}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |