题目内容

13．六安滨河公园喷泉中央有一个强力喷水柱，为了测量喷水柱喷出的水柱的高度，某人在水柱正西方向的A处测得水柱顶端的仰角为45°，沿A处向南偏东30°前进50米到达点B处，在B处测得水柱顶端的仰角为30°，则水柱的高度是（　　）
A．15mB．30mC．25mD．50m

分析 如图所示，设水柱CD的高度为h．在Rt△ACD中，由∠DAC=45°，可得AC=h．由∠BAE=30°，可得∠CAB=60°．在Rt△BCD中，∠CBD=30°，可得BC=$\sqrt{3}$h．在△ABC中，由余弦定理可得：BC2=AC2+AB2-2AC•ABcos60°．代入即可得出．

解答 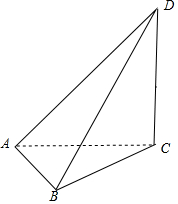解：如图所示
设水柱CD的高度为h．
在Rt△ACD中，∵∠DAC=45°，∴AC=h．
在Rt△BCD中，∠CBD=30°，∴BC=$\sqrt{3}$h．
在△ABC中，∠CAB=60°，由余弦定理可得：
BC2=AC2+AB2-2AC•ABcos60°．
∴3h2=h2+502-$2×50h×\frac{1}{2}$，
化为2h2+50h-2500=0，解得h=25．
故选C，

点评 本题考查了直角三角形的边角关系、余弦定理，考查了推理能力和计算能力，属于中档题．

练习册系列答案
相关题目
3．已知定义在R上的奇函数f（x）满足f（x）=x2-2x-3（x＞0）．
（Ⅰ） 若函数g（x）=|f（x）|-a有4个零点，求实数a的取值范围；
（Ⅱ） 求|f（x+1）|≤4的解集．
4．将函数f（x）=3sin4x+$\sqrt{3}$cos4x图象上所有点的横坐标变为原来的2倍，再向右平移$\frac{π}{6}$个单位长度，得到函数y=g（x）的图象，则y=g（x）的图象的一条对称轴方程是（　　）
A．x=$\frac{π}{12}$B．x=$\frac{π}{6}$C．x=$\frac{π}{3}$D．x=$\frac{2π}{3}$
1．设Sn为各项不相等的等差数列an的前n 项和，已知a3a8=3a11，S3=9．
（1）求数列{an}的通项公式；
（2）求数列{$\frac{1}{{{a_n}{a_{n+1}}}}$}的前n 项和Tn．
8．已知椭圆$E：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的短轴长为2，离心率为$\frac{{2\sqrt{5}}}{5}$，抛物线G：y2=2px（p＞0）的焦点F与椭圆E的右焦点重合，若斜率为k的直线l过抛物线G的焦点F与椭圆E相交于A，B两点，与抛物线G相交于C，D两点．
（Ⅰ）求椭圆E及抛物线G的方程；
（Ⅱ）是否存在实数λ，使得$\frac{1}{{|{AB}|}}+\frac{λ}{{|{CD}|}}$为常数？若存在，求出λ的值，若不存在，请说明理由．
18．已知圆O的半径为2，它的内接三角形ABC满足c2-a2=4（$\sqrt{3}$c-b）sinB，其中a，b，c分别为角A，B，C的对边．
（Ⅰ）求角A；
（Ⅱ）求三角形ABC面积S的最大值．
5．将正整数12分解成两个正整数的乘积有1×12，2×6，3×4三种，其中3×4是这三种分解中两数差的绝对值最小的，我们称3×4为12的最佳分解．当p×q（p≤q且pq∈N*，）是正整数n的最佳分解时，我们定义函数f（n）=q-p，例如f（12）=4-3=1．数列{f（3n）}的前100项和为350-1．
2．大数据时代出现了滴滴打车服务，二胎政策的放开使得家庭中有两个小孩的现象普遍存在，某城市关系要好的A，B，C，D四个家庭各有两个小孩共8人，准备使用滴滴打车软件，分乘甲、乙两辆汽车出去游玩，每车限坐4名（乘同一辆车的4名小孩不考虑位置），其中A户家庭的孪生姐妹需乘同一辆车，则乘坐甲车的4名小孩恰有2名来自于同一个家庭的乘坐方式共有（　　）
A．18种B．24种C．36种D．48种
3．已知角θ的顶点与原点重合，始边与x轴的正半轴重合，终边在直线$y=-\sqrt{3}x$上，则sin2θ=（　　）
A．$\frac{1}{2}$B．$\frac{{\sqrt{3}}}{2}$C．$-\frac{1}{2}$D．$-\frac{{\sqrt{3}}}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网