题目内容
13.在△ABC中,角A,B,C的对边长是a,b,c公差为1的等差数列,且a+b=2ccosA.(Ⅰ)求证:C=2A;
(Ⅱ)求a,b,c.
分析 (Ⅰ)由a+b=2ccosA.利用正弦定理可证C=2A.
(Ⅱ)由a,b,c公差为1的等差数列,得a=b-1,c=b+1,由余弦定理得a2=b2+c2-2bccosA,利用正弦定理可求a,b,c的值.
解答 (Ⅰ)证明:由已知a+b=2ccosA及正弦定理得sinA+sinB=2sinCcosA…①,
又sinB=sin(A+C)=sinAcosC+cosAsinC…②
把②代入①得:sinA+sinAcosC+cosAsinC=2sinCcosA,
整理得:sinA=sin(C-A)
又∵0<A<π,0<C-A<π,
∴A=C-A
故C=2A.
(Ⅱ)由已知得a=b-1,c=b+1,由余弦定理得a2=b2+c2-2bccosA,
整理得:b+4=2(b+1)cosA①
由(Ⅰ)知C=2A,得sinC=sin2A=2sinAcosA,
由正弦定理得c=2acosA即cosA=$\frac{c}{2a}$=$\frac{b+1}{2(b-1)}$②
由①②整理得:b=5,
∴a=4,b=5,c=6.
点评 本题考查三角形的解法,正弦定理以及余弦定理的应用,考查计算能力.

练习册系列答案
相关题目
3.抽样统计甲、乙两名学生的5次训练成绩(单位:分),结果如下:
则成绩较为稳定(方差较小)的那位学生成绩的方差为20.
| 学生 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 甲 | 65 | 80 | 70 | 85 | 75 |
| 乙 | 80 | 70 | 75 | 80 | 70 |
4.执行如图所示的程序框图后,输出的值为4,则p的取值范围是( )


| A. | $\frac{3}{4}<p≤\frac{7}{8}$ | B. | $p>\frac{5}{16}$ | C. | $\frac{7}{8}≤p<\frac{5}{16}$ | D. | $\frac{7}{8}<p≤\frac{5}{16}$ |
1.若复数z满足i•z=$\frac{1}{2}$(1+i),则z的虚部是( )
| A. | -$\frac{1}{2}$i | B. | $\frac{1}{2}$i | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
18.命题“?x0∈(1,+∞),x02+2x0+2≤0”的否定形式是( )
| A. | $?x∈(1,+∞),x_0^2+2{x_0}+2>0$ | B. | $?x∈({-∞,1}],x_0^2+2{x_0}+2>0$ | ||
| C. | $?{x_0}∈(1,+∞),x_0^2+2{x_0}+2>0$ | D. | $?{x_0}∈({-∞,1}],x_0^2+2{x_0}+2>0$ |
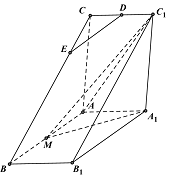 如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.