题目内容

1．若（2x-$\frac{1}{x}$）n展开式的第五项为常数，展开式中二顶式系数最大的项是第五项．

分析 先求得n=8，在二项展开式的通项公式中，令x的幂指数等于0，求出r的值，即可求得常数项．

解答 解：∵（2x-$\frac{1}{x}$）n展开式的第五项为T5=${C}_{n}^{4}$•（2x）n-4•x-4=2n-4•${C}_{n}^{4}$•xn-8 为常数，
∴n=8，故展开式中二顶式系数最大的项是第五项T5=${C}_{8}^{4}$•24，
故答案为：五．

点评 本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题．

练习册系列答案
相关题目
11．已知△ABC中，AC=2，AB=4，点P满足$\overrightarrow{AP}$=x$\overrightarrow{AC}$+y$\overrightarrow{AB}$，x+2y=1（x≥0，y≥0），且|$\overrightarrow{AP}$|的最小值为$\sqrt{3}$，则$\overrightarrow{PA}$•（$\overrightarrow{PB}$+$\overrightarrow{PC}$）的最小值=-$\frac{25}{8}$．
12．已知P，Q，R是圆x2+y2-2x-8=0上不同三点，它们到直线l：x+$\sqrt{3}$y+7=0的距离分别为x1，x2，x3，若x1，x2，x3成等差数列，则公差的最大值为（　　）
A．1B．2C．3D．4
9．已知cos（α+2β）=$\frac{1}{5}$，cosα=$\frac{2}{5}$，则tan（α+β）tanβ=$\frac{1}{3}$．
16．A处存放电线杆40根，从与A相距1000米的B处起，沿AB方向每隔50米架设一根电线杆，一辆车一次能运4根，全部运完返回A处后，这辆车所运行的全部路程是多少千米？
6．函数f（x）=ln$\frac{1}{（2-x）^{2}}$的大致图象是（　　）
A．B．C．D．
13．已知点A（5，m），B（1，2），|$\overrightarrow{AB}$|=5，则m=-1或5．
10．设等差数列{an}的前n项和为Sn，且a4-a2=8，S10=190．求数列{an}的通项公式an．
3．如图，正方体ABCD-A1B1C1D1中，棱长为1，点P在体对角线上，PB=$\frac{1}{3}$PB′，则P点坐标为（　　）
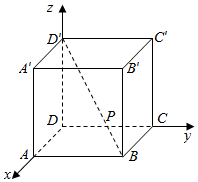
A．（$\frac{1}{3}$$，\frac{1}{3}$，$\frac{1}{3}$）B．（$\frac{2}{3}$，$\frac{2}{3}$，$\frac{2}{3}$）C．（$\frac{5}{6}$，$\frac{5}{6}$，$\frac{1}{6}$）D．（$\frac{2}{3}$，$\frac{2}{3}$，$\frac{1}{3}$）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网