题目内容
9.已知cos(α+2β)=$\frac{1}{5}$,cosα=$\frac{2}{5}$,则tan(α+β)tanβ=$\frac{1}{3}$.分析 利用同角三角函数的基本关系,两角和差的余弦公式求得cos(α+β)cosβ 和sin(α+β)sinβ 的值,可得要求式子的值.
解答 解:∵cos(α+2β)=$\frac{1}{5}$,cosα=$\frac{2}{5}$,∴cos[(α+β)+β]=cos(α+β)cosβ-sin(α+β)sinβ=$\frac{1}{5}$ ①,
cosα=cos[(α+β)-β]=cos(α+β)cosβ+sin(α+β)sinβ=$\frac{2}{5}$ ②,
根据①②求得cos(α+β)cosβ=$\frac{3}{10}$,sin(α+β)sinβ=$\frac{1}{10}$,
∴tan(α+β)tanβ=$\frac{sin(α+β)sinβ}{cos(α+β)cosβ}$=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 本题主要考查同角三角函数的基本关系,两角和差的余弦公式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.参数方程$\left\{\begin{array}{l}{x=sinθ+cosθ}\\{y=sinθcosθ}\end{array}\right.$(θ为参数)表示的曲线为( )
| A. | 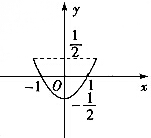 | B. | 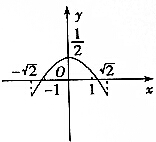 | ||
| C. | 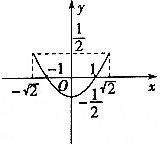 | D. | 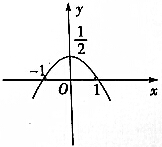 |
17.已知x,y满足不等式组$\left\{\begin{array}{l}{x-y≤1}\\{x+2y≤2}\\{x≥1}\end{array}\right.$,且z=2x-y+a(a为常数)的最大值为2,则z的最小值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{7}{6}$ | D. | $\frac{7}{6}$ |
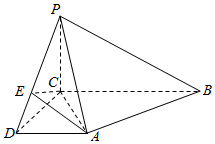 如图,在四棱锥P-ABCD中,AD∥BC,且BC=2AD,AD⊥CD,PB⊥CD,点E在棱PD上,且PE=2ED.
如图,在四棱锥P-ABCD中,AD∥BC,且BC=2AD,AD⊥CD,PB⊥CD,点E在棱PD上,且PE=2ED.