题目内容
已知函数y=
，求：
（1）函数的定义域、值域；
（2）判断函数的奇偶性．
| 2x+2-x |
| 2 |
（1）函数的定义域、值域；
（2）判断函数的奇偶性．
考点：函数奇偶性的判断,函数的定义域及其求法,函数的值域
专题：函数的性质及应用
分析：（1）函数y=
的定义域为R，利用基本不等式的性质即可得出值域．
（2）由于f（-x）=f（x），即可得出奇偶性．
| 2x+2-x |
| 2 |
（2）由于f（-x）=f（x），即可得出奇偶性．
解答：
解：（1）函数y=
的定义域为R，
∵2x+2-x≥2
=2，当且仅当x=0时取等号．
∴y≥1，因此函数的值域为：[1，+∞）．
（2）∵f（-x）=
=f（x），定义域为R，
∴函数f（x）为偶函数．
| 2x+2-x |
| 2 |
∵2x+2-x≥2
| 2x•2-x |
∴y≥1，因此函数的值域为：[1，+∞）．
（2）∵f（-x）=
| 2-x+2x |
| 2 |
∴函数f（x）为偶函数．
点评：本题考查了函数的奇偶性、单调性、基本不等式的性质，属于基础题．
练习册系列答案
相关题目
下列函数既是奇函数，又在区间[-1，1]上单调递减的是（ ）
| A、f（x）=sinx | ||
| B、f（x）=-|x+1| | ||
C、f（x）=
| ||
D、f（x）=ln
|
方程x2-4|x|-3=m有四个解的m的取值范围是（ ）
| A、（-7，-3） |
| B、（0，7） |
| C、[0，7） |
| D、[-7，-3） |
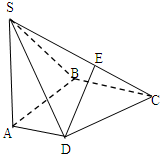四棱锥S-ABCD中，底面ABCD为直角梯形，AB垂直于AD和BC，SA⊥面ABCD，SA=AB=BC=2，AD=1．求：