题目内容
定积分
[
-x]dx= .
| ∫ | 2 0 |
| 1-(x-1)2 |
考点:定积分
专题:计算题,选作题
分析:将定积分分为两个积分的和,再分别求出定积分,即可得到结论.
解答:
解:
[
-x]dx=
dx+
(-x)dx…(*)
∵
dx表示以(1,0)为圆心,以1为半径的圆在第一象限内所围成的面积,
即为该圆的面积的一半.
∴
dx=
.
故(*)的值为
+
d(-
)=
-2.
即分
[
-x]dx=
-2.
| ∫ | 2 0 |
| 1-(x-1)2 |
| ∫ | 2 0 |
| 1-(x-1)2 |
| ∫ | 2 0 |
∵
| ∫ | 2 0 |
| 1-(x-1)2 |
即为该圆的面积的一半.
∴
| ∫ | 2 0 |
| 1-(x-1)2 |
| π |
| 2 |
故(*)的值为
| π |
| 2 |
| ∫ | 2 0 |
| x2 |
| 2 |
| π |
| 2 |
即分
| ∫ | 2 0 |
| 1-(x-1)2 |
| π |
| 2 |
点评:本题考查定积分的几何意义,考查定积分的计算,考查定积分的性质,属于基础题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
设复数z=1+ai(a∈R,i是虚数单位),若M{x|x>2},使|z|∈CRM成立的a的取值范围是( )
A、[-
| ||||
B、[-
| ||||
| C、[-1.1] | ||||
| D、[-2.2] |
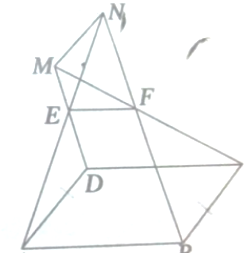 如图所示,若ABCD为平行四边形,EF∥AB,AE与BF相交于点N,DE与CF相交于点M.求证:MN∥AD.
如图所示,若ABCD为平行四边形,EF∥AB,AE与BF相交于点N,DE与CF相交于点M.求证:MN∥AD. 如图,圆O是△ABC的外接圆,∠BAC的平分线交BC于点F,D是AF的延长线与⊙O的交点,AC的延线与⊙O的切线DE交于点E.
如图,圆O是△ABC的外接圆,∠BAC的平分线交BC于点F,D是AF的延长线与⊙O的交点,AC的延线与⊙O的切线DE交于点E.