题目内容
设a=
,b=sin85°-
cos85°,c=2(sin47°sin66°-sin24°sin43°)则a、b、c的大小关系是( )
| 4tan12.5° |
| 1-tan212.5° |
| 3 |
| A、b>c>a |
| B、a>b>c |
| C、b>a>c |
| D、c>b>a |
考点:三角函数中的恒等变换应用
专题:三角函数的求值,三角函数的图像与性质
分析:首先利用诱导公式进行恒等变换,使a=2tan25°=2
>2sin25°,b=2sin25°,c=2sin23°,进一步利用正弦函数的单调性求出a,b,c的大小.
| sin25° |
| cos25° |
解答:
解:a=
=2tan25°=2
>2sin25°;
b=sin85°-
cos85°=2(sin85°cos60°-cos85°sin60°)=2sin25°;
c=2(sin47°sin66°-sin24°sin43°)=2(sin47°cos24°-cos47°sin24°)=2sin23°;
由于函数y=sinx在[0°,90°]为单调递增函数.
所以:a>b>c,
故选:B.
| 4tan12.5° |
| 1-tan212.5° |
| sin25° |
| cos25° |
b=sin85°-
| 3 |
c=2(sin47°sin66°-sin24°sin43°)=2(sin47°cos24°-cos47°sin24°)=2sin23°;
由于函数y=sinx在[0°,90°]为单调递增函数.
所以:a>b>c,
故选:B.
点评:本题考查的知识要点:三角函数的诱导公式的应用,正弦函数单调性的应用.属于基础题型.

练习册系列答案
相关题目
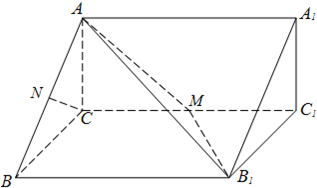 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,CC1=4,M是棱CC1上的一点.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,CC1=4,M是棱CC1上的一点.