题目内容
选派5名学生参加四项环保志愿活动,要求每项活动至少有一人参加,则不同的选派方法共有 种.
考点:排列、组合的实际应用
专题:计算题
分析:分2步分析:①、先将5名学生分成4组,分析可得应该1组有2人,剩余3组每组1人,由组合数公式可得其情况数目,②、由排列数公式计算将分好的4个组对应四项环保志愿活动的情况数目,由乘法原理计算可得答案.
解答:
解:根据题意,分2步分析:
①、先将5名学生分成4组,分析可得应该1组有2人,剩余3组每组1人,
则有C52=10种情况,
②、将分好的4个组对应四项环保志愿活动,有A44=24种情况,
则共有10×24=240种不同的选派方法;
故答案为:240.
①、先将5名学生分成4组,分析可得应该1组有2人,剩余3组每组1人,
则有C52=10种情况,
②、将分好的4个组对应四项环保志愿活动,有A44=24种情况,
则共有10×24=240种不同的选派方法;
故答案为:240.
点评:本题考查分步计数原理的应用,解题时一定要分清做这件事需要分为几步,每一步包含几种方法,看清思路,把几个步骤中数字相乘得到结果.

练习册系列答案
相关题目
若一元二次不等式f(x)>0的解集为{x|-2<x<1},则f(2x)<0的解集为( )
| A、{x|x<-2或x>0} |
| B、{x|x<0或x>2} |
| C、{x|x>0} |
| D、{x|x<0} |

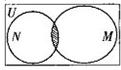 已知全集U=R,集合M={x|-2≤x-1≤2}和N={x|x=2k-1,k=1,2,…}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合的元素共有
已知全集U=R,集合M={x|-2≤x-1≤2}和N={x|x=2k-1,k=1,2,…}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合的元素共有