题目内容
2.在极坐标系中,圆ρ=-2cosθ的圆心C到直线2ρcosθ+ρsinθ-2=0的距离等于$\frac{4\sqrt{5}}{5}$.分析 圆ρ=-2cosθ化为直角坐标方程式,求出圆心C(-1,0),直线2ρcosθ+ρsinθ-2=0化为直角坐标方程,由此利用点到直线的距离公式能求出圆心C到直线的距离.
解答 解:圆ρ=-2cosθ,即ρ2=-2ρcosθ,
化为直角坐标方程得:x2+y2=-2x,即(x+1)2+y2=1.
∴圆心C(-1,0),
∵直线2ρcosθ+ρsinθ-2=0,
∴直线的直角坐标方程为2x+y-2=0,
∴圆心C到直线的距离:
d=$\frac{|2×(-1)+0-2|}{\sqrt{4+1}}$=$\frac{4\sqrt{5}}{5}$.
故答案为:$\frac{4\sqrt{5}}{5}$.
点评 本题考查点到直线的距离的求法,涉及到直角坐标方程、极坐标方程、参数方程的互化、点到直线的距离公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
13.已知某条曲线的参数方程是$\left\{\begin{array}{l}x=2(t+\frac{1}{t})\\ y=2(t-\frac{1}{t})\end{array}$(t是参数),则该曲线是( )
| A. | 直线 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |
7.设P是曲线y=x-$\frac{1}{2}$x2-lnx上的一个动点,记此曲线在点P点处的切线的倾斜角为θ,则θ的取值范围是( )
| A. | ($\frac{π}{2}$,$\frac{3π}{4}$] | B. | [$\frac{π}{4}$,$\frac{3π}{4}$] | C. | [$\frac{3π}{4}$,π) | D. | [0,$\frac{π}{2}$)∪[$\frac{3π}{4}$,π) |
11.把函数f(x)=cos2($\frac{π}{2}$x-$\frac{π}{6}$)的图象向左平移$\frac{1}{3}$个单位后得到的函数为g(x),则以下结论中正确的是( )
| A. | g($\frac{1}{5}$)>g($\frac{8}{5}$)>0 | B. | g($\frac{1}{5}$)$>0>g(\frac{8}{5})$ | C. | g($\frac{8}{5}$)>g($\frac{1}{5}$)>0 | D. | g($\frac{1}{5}$)=g($\frac{8}{5}$)>0 |
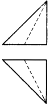
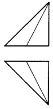
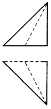
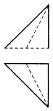
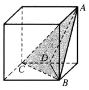 如图是一个正方体,A,B,C为三个顶点,D是棱的中点,则三棱锥A-BCD的正视图,俯视图是(注:选项中的上图是正视图,下图是俯视图)( )
如图是一个正方体,A,B,C为三个顶点,D是棱的中点,则三棱锥A-BCD的正视图,俯视图是(注:选项中的上图是正视图,下图是俯视图)( )