题目内容
己知集合A={x|x2-3x+2<0},B={x|log4x>
},则( )
| 1 |
| 2 |
| A、A∩B=∅ |
| B、B⊆A |
| C、A∩∁RB=R |
| D、A⊆B |
考点:集合的包含关系判断及应用
专题:不等式的解法及应用,集合
分析:解A中的一元二次不等式把集合A化简,解B中的对数不等式把集合B化简,即可判断A与B之间的关系.
解答:
解:解不等式x2-3x+2<0,得1<x<2,
∴A={x|x2-3x+2<0}=(1,2).
由log4x>
,得x>2,
∴B={x|log4x>
}=(2,+∞),
∴A∩B=∅,
故选:A
∴A={x|x2-3x+2<0}=(1,2).
由log4x>
| 1 |
| 2 |
∴B={x|log4x>
| 1 |
| 2 |
∴A∩B=∅,
故选:A
点评:本题考查了集合的包含关系,正确解不等式是关键,属于基础题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
设(2+i)
=3+4i,则z=( )
. |
| z |
| A、1+2i | B、1-2i |
| C、2+i | D、2-i |
已知等比数列{an}中,a2+a3=1,a4+a5=2,则a6+a7等于( )
| A、2 | ||
B、2
| ||
| C、4 | ||
D、4
|
球面上有M、N两点,在过M、N的球的大圆上,
的度数为90°,在过M、N的球小圆上,
的度数为120°,又MN=
cm,则球心到上述球小圆的距离是( )
 |
| MN |
 |
| MN |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1cm |
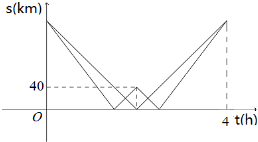 A,B两架直升机同时从机场出发,完成某项救灾物资空投任务.A机到达甲地完成任务后原路返回;B机路过甲地,前往乙地完成任务后原路返回.如图中折线分别表示A,B两架直升机离甲地的距离s与时间t之间的函数关系.假设执行任务过程中A,B均匀速直线飞行,则B机每小时比A机多飞行
A,B两架直升机同时从机场出发,完成某项救灾物资空投任务.A机到达甲地完成任务后原路返回;B机路过甲地,前往乙地完成任务后原路返回.如图中折线分别表示A,B两架直升机离甲地的距离s与时间t之间的函数关系.假设执行任务过程中A,B均匀速直线飞行,则B机每小时比A机多飞行