题目内容
13.命题“对任意实数x∈[2,3],关于x的不等式x2-a≤0恒成立”为真命题的一个必要不充分条件是( )| A. | a≥9 | B. | a≤9 | C. | a≤8 | D. | a≥8 |
分析 命题“对任意实数x∈[2,3],关于x的不等式x2-a≤0恒成立”为真命题,可得a≥[x2]max.
解答 解:命题“对任意实数x∈[2,3],关于x的不等式x2-a≤0恒成立”为真命题,
∴a≥[x2]max=9.
∴命题“对任意实数x∈[2,3],关于x的不等式x2-a≤0恒成立”为真命题的一个必要不充分条件是a≥8.
故选:D.
点评 本题考查了简易逻辑的判定方法、函数的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
1.在下列区间中,函数f(x)=3x-2的零点所在的区间为( )
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
8.设F1,F2分别是椭圆$E:{x^2}+\frac{y^2}{b^2}=1(0<b<1)$的左、右焦点,已知点F1的直线交椭圆E于A,B两点,若|AF1|=2|BF1|,AF2⊥x轴,则椭圆E的方程为( )
| A. | ${x^2}+\frac{{3{y^2}}}{2}=1$ | B. | ${x^2}+\frac{{6{y^2}}}{5}=1$ | C. | ${x^2}+\frac{{5{y^2}}}{4}=1$ | D. | ${x^2}+\frac{{8{y^2}}}{7}=1$ |
18.将3本相同的语文书和2本相同的数学书分给四名同学,每人至少1本,不同的分配方法数有( )
| A. | 24 | B. | 28 | C. | 32 | D. | 36 |
5.过三个点A(1,3),B(4,2),C(1,-1)的圆交y轴于M,N两点,则|MN|=( )
| A. | 2$\sqrt{6}$ | B. | 3$\sqrt{6}$ | C. | 2 | D. | 5$\sqrt{6}$ |
2.命题“若A=B,则A⊆B”与其逆命题、否命题、逆否命题这四个命题中,真命题的个数是( )
| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
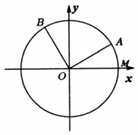 如图,已知单位圆O与x轴正半轴相交于点M,点A,B在单位圆上,其中点A在第一象限,且∠AOB=$\frac{π}{2}$,记∠MOA=α,∠MOB=β.
如图,已知单位圆O与x轴正半轴相交于点M,点A,B在单位圆上,其中点A在第一象限,且∠AOB=$\frac{π}{2}$,记∠MOA=α,∠MOB=β.