题目内容
12．已知直线$l：\frac{x}{a}+\frac{y}{b}=1（{a＞0，b＞0}）$将圆C：x2+y2-2x-4y+4=0平分，则直线l与两坐标轴围成的三角形的面积的最小值为（ ）| A． | 8 | B． | 4 | C． | 2 | D． | 1 |
分析 先确定$\frac{1}{a}$+$\frac{2}{b}$=1，再利用基本不等式，即可得出结论．
解答 解：圆C：x2+y2-2x-4y+4=0的圆心坐标为（1，2），
则$\frac{1}{a}$+$\frac{2}{b}$=1≥2$\sqrt{\frac{2}{ab}}$，∴ab≥8，
∴直线l与两坐标轴围成的三角形的面积S=$\frac{1}{2}ab$≥4，
∴直线l与两坐标轴围成的三角形的面积的最小值是4，
故选B．
点评 本题考查直线与圆的位置关系，考查基本不等式的运用，属于中档题．
练习册系列答案
相关题目
2．平面直角坐标系中，椭圆C中心在原点，焦点F1、F2在x轴上，离心率为$\frac{{\sqrt{3}}}{3}$．过点F1的直线l与C交于A、B两点，且△ABF2周长为$4\sqrt{3}$，那么C的方程为（ ）
| A． | $\frac{x^2}{3}+{y^2}=1$ | B． | $\frac{x^2}{3}+\frac{y^2}{2}=1$ | C． | $\frac{x^2}{12}+\frac{y^2}{4}=1$ | D． | $\frac{x^2}{12}+\frac{y^2}{8}=1$ |
7．要想得到函数y=sin2x+1的图象，只需将函数y=cos2x的图象（ ）
| A． | 向左平移$\frac{π}{4}$个单位，再向上平移1个单位 | |
| B． | 向右平移$\frac{π}{4}$个单位，再向上平移1个单位 | |
| C． | 向左平移$\frac{π}{2}$个单位，再向下平移1个单位 | |
| D． | 向右平移$\frac{π}{2}$个单位，再向上平移1个单位 |
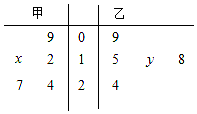如图，茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩（单位：分）．已知甲组数据的中位数为15，乙组数据的平均数为16.8，则x+y的值为（ ）
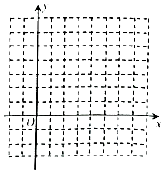某工厂要安排生产Ⅰ、Ⅱ两种产品，这些产品要在A、B、C、D四种不同的设备上加工，按工艺规定，在一天内，产品Ⅰ每件在A、B、C、D设备上需要加工时间分别是2、2、3、0小时，产品Ⅱ每件在A、B、C、D设备上需要加工时间分别是4、1、0、3小时，A、B、C、D设备最长使用时间分别是16、8、9、9小时．设计划每天生产产品Ⅰ的数量为x（件），产品Ⅱ的数量为y（件）．（x，y∈N）