题目内容
3.在平面直角坐标系中,动圆P截直线3x-y=0和3x+y=0所得弦长分别为8,4,则动圆圆心P到直线$x+2y+\sqrt{5}=0$的距离的最小值为3.分析 动圆截直线3x-y=0和3x+y=0所得的弦长分别为8,4,利用点到直线的距离公式、垂径定理可得点P的轨迹方程,再利用点到直线的距离公式,可得结论.
解答 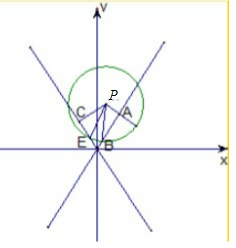 解:如图所示,设点P(x,y),由条件可得,AB=4,EC=2
解:如图所示,设点P(x,y),由条件可得,AB=4,EC=2
由点到直线的距离公式,垂径定理可得$\frac{(3x-y)^{2}}{10}$+16=$\frac{(3x+y)^{2}}{10}$+4,化简可得,xy=10.
∴点P的轨迹方程为xy=10.
动圆圆心P到直线$x+2y+\sqrt{5}=0$的距离d=$\frac{|x+2y+\sqrt{5}|}{\sqrt{5}}$≥3,
∴动圆圆心P到直线$x+2y+\sqrt{5}=0$的距离的最小值为3,
故答案为3.
点评 本题以直线与圆相交为载体,考查轨迹方程,解题的关键是利用圆的特殊性,借助于垂径定理求解.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
11.在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在l上,若圆C上存在点M,使|MA|=2|MO|,则圆心C的横坐标的取值范围为( )
| A. | $[{0,\frac{12}{5}}]$ | B. | [0,1] | C. | $[{1,\frac{12}{5}}]$ | D. | $({0,\frac{12}{5}})$ |
18.已知函数f(x)=x2-4x+3,g(x)=m(x-1)+2(m>0),若存在x1∈[0,3],使得对任意的x2∈[0,3],都有f(x1)=g(x2),则实数m的取值范围是( )
| A. | $({0,\frac{1}{2}}]$ | B. | (0,3] | C. | $[{\frac{1}{2},3}]$ | D. | [3,+∞) |
15.圆C1:x2+y2+2x+4y+1=0与圆C2:x2+y2-4x+4y-17=0的位置关系是( )
| A. | 内切 | B. | 外切 | C. | 相交 | D. | 相离 |
12.已知直线$l:\frac{x}{a}+\frac{y}{b}=1({a>0,b>0})$将圆C:x2+y2-2x-4y+4=0平分,则直线l与两坐标轴围成的三角形的面积的最小值为( )
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
13.已知全集U={1,2,3,4,5,6,7,8},集合A={2,3,5,6},集合B={1,3,4,6},则A∪(∁UB)=( )
| A. | {2,5} | B. | {2,5,7,8} | C. | {2,3,5,6,7,8} | D. | {1,2,3,4,5,6} |