题目内容
20.已知$sin({α+β})=\frac{1}{5},sin({α-β})=\frac{3}{5}$,求$\frac{tanα}{tanβ}$的值.分析 利用两角和与差的正弦函数公式化简已知,两式相加减化简,进而利用同角三角函数基本关系式即可计算得解.
解答 解:∵$sin({α+β})=\frac{1}{5},sin({α-β})=\frac{3}{5}$,
∴sinαcosβ+cosαsinβ=$\frac{1}{5}$,sinαcosβ-cosαsinβ=$\frac{3}{5}$,
∴两式相加,可得:sinαcosβ=$\frac{2}{5}$,①两式相减,可得:cosαsinβ=-$\frac{2}{5}$,②
∴①÷②可得:$\frac{tanα}{tanβ}$=-1.
点评 本题主要考查了两角和与差的正弦函数公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
10.若函数f(x)=a(x2+$\frac{2}{x}$)-lnx(a>0)有唯一零点x0,且m<x0<n(m,n为相邻整数),其中自然对数e=2.71828…,则m+n的值为( )
| A. | 1 | B. | 3 | C. | 5 | D. | 7 |
11.在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在l上,若圆C上存在点M,使|MA|=2|MO|,则圆心C的横坐标的取值范围为( )
| A. | $[{0,\frac{12}{5}}]$ | B. | [0,1] | C. | $[{1,\frac{12}{5}}]$ | D. | $({0,\frac{12}{5}})$ |
15.圆C1:x2+y2+2x+4y+1=0与圆C2:x2+y2-4x+4y-17=0的位置关系是( )
| A. | 内切 | B. | 外切 | C. | 相交 | D. | 相离 |
12.已知直线$l:\frac{x}{a}+\frac{y}{b}=1({a>0,b>0})$将圆C:x2+y2-2x-4y+4=0平分,则直线l与两坐标轴围成的三角形的面积的最小值为( )
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
10.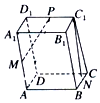 如图所示,在平行六面体ABCD-A1B1C1D1中,设$\overrightarrow{A{A_1}}=\overrightarrow a$,$\overrightarrow{AB}=\overrightarrow b$,$\overrightarrow{AD}=\overrightarrow c$,M,N,P分别是AA1,BC,C1D1的中点,则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=( )
如图所示,在平行六面体ABCD-A1B1C1D1中,设$\overrightarrow{A{A_1}}=\overrightarrow a$,$\overrightarrow{AB}=\overrightarrow b$,$\overrightarrow{AD}=\overrightarrow c$,M,N,P分别是AA1,BC,C1D1的中点,则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=( )
 如图所示,在平行六面体ABCD-A1B1C1D1中,设$\overrightarrow{A{A_1}}=\overrightarrow a$,$\overrightarrow{AB}=\overrightarrow b$,$\overrightarrow{AD}=\overrightarrow c$,M,N,P分别是AA1,BC,C1D1的中点,则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=( )
如图所示,在平行六面体ABCD-A1B1C1D1中,设$\overrightarrow{A{A_1}}=\overrightarrow a$,$\overrightarrow{AB}=\overrightarrow b$,$\overrightarrow{AD}=\overrightarrow c$,M,N,P分别是AA1,BC,C1D1的中点,则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=( )| A. | $\frac{3}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{3}{2}\overrightarrow c$ | B. | $\overrightarrow a+\frac{1}{2}\overrightarrow c$ | C. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | D. | $\frac{3}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{1}{2}\overrightarrow c$ |
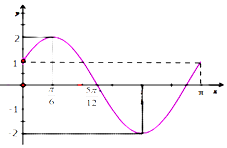 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|ϕ|<\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|ϕ|<\frac{π}{2}$)的部分图象如图所示.