题目内容
2.已知函数f(x)=lnx+ax2,g(x)=$\frac{1}{x}$+x+b,且直线y=-$\frac{1}{2}$是函数f(x)的一条切线.(Ⅰ)求a的值;
(Ⅱ)对任意的x1∈[1,$\sqrt{e}$],都存在x2∈[1,4],使得f(x1)=g(x2),求b的取值范围.
分析 (Ⅰ)设直线y=-$\frac{1}{2}$与f(x)相切于点(x0,lnx0+ax02)(x0>0),求得f(x)的导数,由已知切线方程,可得切线的斜率为0,及f(x0)=-$\frac{1}{2}$,解方程可得a的值;
(Ⅱ)由题意可得f(x)在[1,$\sqrt{e}$]的值域包含于g(x)在[1,4]的值域.运用导数,
求得单调性,可得值域,再由不等式解得即可.
解答 解:(Ⅰ)设直线y=-$\frac{1}{2}$与f(x)相切于点(x0,lnx0+ax02)(x0>0),
f′(x)=$\frac{1}{x}$+2ax=$\frac{2a{x}^{2}+1}{x}$,
依题意得$\left\{\begin{array}{l}{\frac{2a{{x}_{0}}^{2}+1}{{x}_{0}}=0}\\{ln{x}_{0}+a{{x}_{0}}^{2}=-\frac{1}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{{x}_{0}=1}\\{a=-\frac{1}{2}}\end{array}\right.$,
所以a=-$\frac{1}{2}$,经检验:a=-$\frac{1}{2}$符合题意;
(Ⅱ)由(Ⅰ)得f(x)=lnx-$\frac{1}{2}$x2,
所以f′(x)=$\frac{1}{x}$-x=$\frac{1-{x}^{2}}{x}$,
当x∈(1,$\sqrt{e}$]时,f′(x)<0,所以f(x)在[1,$\sqrt{e}$]上单调递减,
所以当x∈[1,$\sqrt{e}$]时,f(x)min=f($\sqrt{e}$)=$\frac{1}{2}$-$\frac{1}{2}$e,f(x)max=f(1)=-$\frac{1}{2}$,
$g'(x)=-\frac{1}{x^2}+1=\frac{{-1+{x^2}}}{x^2}$,
当x∈(1,4]时,g′(x)>0,所以g(x)在[1,4]上单调递增,
所以当x∈(1,4]时,g(x)min=g(1)=2+b,$g{(x)_{max}}=g(4)=\frac{17}{4}+b$,
依题意得$[\frac{1}{2}-\frac{e}{2},-\frac{1}{2}]⊆[2+b,\frac{17}{4}+b]$,
即有$\left\{{\begin{array}{l}{2+b≤\frac{1}{2}-\frac{e}{2}}\\{\frac{17}{4}+b≥-\frac{1}{2}}\end{array}}\right.$,
解得$-\frac{19}{4}≤b≤-\frac{3}{2}-\frac{e}{2}$.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查任意存在性问题的解法,注意运用转化思想,转化为函数的值域包含关系,考查运算能力,属于中档题.

| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
| A. | {2,5} | B. | {2,5,7,8} | C. | {2,3,5,6,7,8} | D. | {1,2,3,4,5,6} |
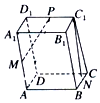 如图所示,在平行六面体ABCD-A1B1C1D1中,设$\overrightarrow{A{A_1}}=\overrightarrow a$,$\overrightarrow{AB}=\overrightarrow b$,$\overrightarrow{AD}=\overrightarrow c$,M,N,P分别是AA1,BC,C1D1的中点,则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=( )
如图所示,在平行六面体ABCD-A1B1C1D1中,设$\overrightarrow{A{A_1}}=\overrightarrow a$,$\overrightarrow{AB}=\overrightarrow b$,$\overrightarrow{AD}=\overrightarrow c$,M,N,P分别是AA1,BC,C1D1的中点,则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=( )| A. | $\frac{3}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{3}{2}\overrightarrow c$ | B. | $\overrightarrow a+\frac{1}{2}\overrightarrow c$ | C. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | D. | $\frac{3}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{1}{2}\overrightarrow c$ |
| A. | lna>-b-1 | B. | lna≥-b-1 | C. | lna≤-b-1 | D. | lna<-b-1 |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
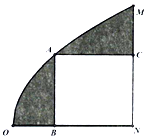 某校一块空地的轮廓线如图所示,曲线段OM是以O为顶点,ON为对称轴且开口向右的抛物线的一段,已知ON=4(单位:百米),MN=4.现计划在该区域内围出一块矩形地块ABNC作为学生活动区域,其余阴影部分进行绿化建设,其中A在曲线段OM上,C在MN上,B在ON上.
某校一块空地的轮廓线如图所示,曲线段OM是以O为顶点,ON为对称轴且开口向右的抛物线的一段,已知ON=4(单位:百米),MN=4.现计划在该区域内围出一块矩形地块ABNC作为学生活动区域,其余阴影部分进行绿化建设,其中A在曲线段OM上,C在MN上,B在ON上.