题目内容
市场营销人员对过去几年某商品的价格及销售数量的关系作数据分析发现有如下规律:该商品的价格每上涨x%(x>0),销售量就减少kx%(其中k为正常数).目前,该商品定价a元,统计其销售数量为b个.
(1)当k=
时,该商品的价格上涨多少,就能使销售的总金额达到最大?
(2)在适当的涨价过程中,求使销售总金额不断增加时的k的取值范围.
(1)当k=
| 1 |
| 2 |
(2)在适当的涨价过程中,求使销售总金额不断增加时的k的取值范围.
考点:函数模型的选择与应用
专题:函数的性质及应用
分析:(1)当k=
时,减函数函数关系式即可.
(2)根据二次函数的图象和性质即可得到结论.
| 1 |
| 2 |
(2)根据二次函数的图象和性质即可得到结论.
解答:
解析:(1)当k=
时,销售的总金额y=a(1+x%)?b(1-kx%)=-
(x%+1)(x%-2)
=-
(x%-
)2+
ab≤
ab,
答:该商品的价格上涨50%的时候,销售的总金额达到最大值
ab元.
(2)y=a(1+x%)?b(1-kx%)=ab(1+x%)(1-kx%)=
[kx2-100(k-1)x+10000](k>0)
据题意,就是使函数在(0,+∞)上单增,则
≤0⇒0<k≤1
答:使销售总金额不断增加时的k的取值范围是(0,1].
| 1 |
| 2 |
| ab |
| 2 |
=-
| ab |
| 2 |
| 1 |
| 2 |
| 9 |
| 8 |
| 9 |
| 8 |
答:该商品的价格上涨50%的时候,销售的总金额达到最大值
| 9 |
| 8 |
(2)y=a(1+x%)?b(1-kx%)=ab(1+x%)(1-kx%)=
| ab |
| 10000 |
据题意,就是使函数在(0,+∞)上单增,则
| 100(k-1) |
| 2k |
答:使销售总金额不断增加时的k的取值范围是(0,1].
点评:本题主要考查函数的应用问题,根据条件建立二次函数关系结合二次函数的图象和性质是解决本题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
某房地产公司计划出租70套相同的公寓房.当每套房月租金定为3000元时,这70套公寓能全租出去;当月租金每增加50元时(设月租金均为50元的整数倍),就会多一套房子不能出租.设租出的每套房子每月需要公司花费100元的日常维修等费用(设租不出的房子不需要花这些费用).要使公司获得最大利润,每套房月租金应定为( )
| A、3000 | B、3300 |
| C、3500 | D、4000 |
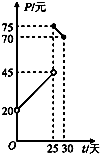 某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系用如图表示,该商品在30天内日销售量Q(件)与时间t(天)之间的关系如下表:
某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系用如图表示,该商品在30天内日销售量Q(件)与时间t(天)之间的关系如下表: 某车间共有6名工人,他们某日加工零件葛素的茎叶图如图所示,其中茎为十位数,叶为个位数日加工零件大于样本均值的工人为优秀工人,从该车间6名工人中,任取2人,则恰由1名优秀工人的概率为( )
某车间共有6名工人,他们某日加工零件葛素的茎叶图如图所示,其中茎为十位数,叶为个位数日加工零件大于样本均值的工人为优秀工人,从该车间6名工人中,任取2人,则恰由1名优秀工人的概率为( )