题目内容
20.用反证法证明命题:“在一个三角形的三个内角中,至少有二个锐角”时,假设部分的内容应为在一个三角形的三个内角中,至多有一个锐角.分析 用反证法证明数学命题时,应先假设结论的否定成立.
解答 解:根据反证法的步骤,假设是对原命题结论的否定,“在一个三角形的三个内角中,至少有2个锐角”的否定:在一个三角形的三个内角中,至多有一个锐角.
故答案为:在一个三角形的三个内角中,至多有一个锐角.
点评 本题考查反证法的概念,逻辑用语,否命题与命题的否定的概念,逻辑词语的否定.一些正面词语的否定:“是”的否定:“不是”;“能”的否定:“不能”;“都是”的否定:“不都是”;“至多有一个”的否定:“至少有两个”;“至少有一个”的否定:“一个也没有”;“是至多有n个”的否定:“至少有n+1个”;“任意的”的否定:“某个”;“任意两个”的否定:“某两个”;“所有的”的否定:“某些”.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
11.阅读如下程序框图,运行相应的程序,则程序运行后输出的结果为( )
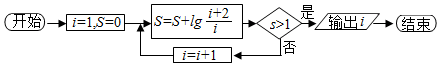
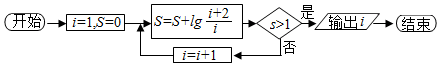
| A. | 4 | B. | 11 | C. | 13 | D. | 15 |
8.函数f(x)是定义在(0,+∞)上的单调函数,且对定义域内的任意x,均有f(f(x)-lnx-x3)=2,则f(e)=( )
| A. | e3+1 | B. | e3+2 | C. | e3+e+1 | D. | e3+e+2 |
15.已知函数f(x)=x|x-2|,x∈R,若方程f(x)=a-|x-1|恰有5个互异的实数根,则实数a的取值范围是( )
| A. | (1,$\frac{5}{4}$) | B. | ($\frac{5}{4}$,+∞) | C. | (1,+∞) | D. | (-∞,$\frac{5}{4}$) |
12.运行如图的程序框图,若输出的y值随着输入的x的增大而增大,则a的取值不可能是( )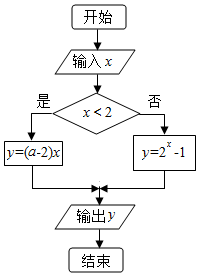

| A. | $\frac{5}{2}$ | B. | $\frac{7}{2}$ | C. | 3 | D. | 4 |
9.已知点M是△ABC所在平面内的一点,且满足5$\overrightarrow{AM}$=$\overrightarrow{AB}$+2$\overrightarrow{AC}$,则△AMB与△ABC的面积比为( )
| A. | $\frac{5}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{7}{5}$ | D. | $\frac{5}{7}$ |
10.把复数z的共轭复数记作$\overline z$,已知(3-4i)$\overline z$=1+2i,则z=( )
| A. | $\frac{1}{5}$+$\frac{2}{5}$i | B. | -$\frac{1}{5}$+$\frac{2}{5}$i | C. | -$\frac{1}{5}$-$\frac{2}{5}$i | D. | $\frac{1}{5}$-$\frac{2}{5}i$ |
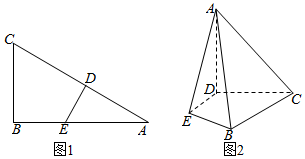 已知直角三角形ABC中,AC=6,BC=3,∠ABC=90°,点D,E分别是边AC,AB上的动点(不含A点),且满足$\frac{AD}{AE}=\frac{{\sqrt{3}}}{2}$(图1).将△ADE沿DE折起,使得平面ADE⊥平面BCDE,连结AB、AC(图2).
已知直角三角形ABC中,AC=6,BC=3,∠ABC=90°,点D,E分别是边AC,AB上的动点(不含A点),且满足$\frac{AD}{AE}=\frac{{\sqrt{3}}}{2}$(图1).将△ADE沿DE折起,使得平面ADE⊥平面BCDE,连结AB、AC(图2).