题目内容
8.函数f(x)是定义在(0,+∞)上的单调函数,且对定义域内的任意x,均有f(f(x)-lnx-x3)=2,则f(e)=( )| A. | e3+1 | B. | e3+2 | C. | e3+e+1 | D. | e3+e+2 |
分析 由题意得f(x)-lnx-x3是定值,令f(x)-lnx-x3=t,得到lnt+t3+t=2,求出t的值,从而求出f(x)的表达式,求出f(e)即可.
解答 解:∵函数f(x)对定义域内的任意x,均有f(f(x)-lnx-x3)=2,
则f(x)-lnx-x3是定值,
不妨令f(x)-lnx-x3=t,
则f(t)=lnt+t3+t=2,解得:t=1,
∴f(x)=lnx+x3+1,
∴f(e)=lne+e3+1=e3+2,
故选:B
点评 本题考查了求函数的解析式问题,考查函数的单调性问题,求出f(x)的表达式是解题的关键,本题是一道中档题.

练习册系列答案
相关题目
16.执行如图所示的程序框图,若输出的S值为-4,则条件框内应填写( )


| A. | i>3? | B. | i<5? | C. | i>4? | D. | i<4? |
13.按如图所示的程序框图运行后,输出的结果是63,则判断框中的整数M的值是( )
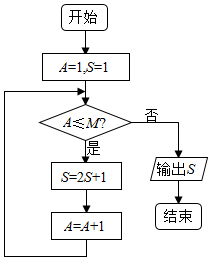

| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
18.已知集合A={1,a},B={1,2,3},则“A⊆B”是“a=3”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
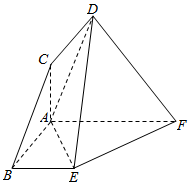 如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA=$\frac{π}{3}$,ABEF为直角梯形,BE∥AF,∠BAF=$\frac{π}{2}$,BE=2,AF=3,平面ABCD⊥平面ABEF.
如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA=$\frac{π}{3}$,ABEF为直角梯形,BE∥AF,∠BAF=$\frac{π}{2}$,BE=2,AF=3,平面ABCD⊥平面ABEF.