题目内容
10.双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{4}$=1的焦点为F1,F2,点P为其上的动点,当∠F1PF2为钝角时,点P横坐标的取值范围是(-$\sqrt{6}$,-2)∪(2,$\sqrt{6}$).分析 求得双曲线的焦点坐标,设双曲线上一点P(x,y),若双曲线上一点P使得∠F1PF2为钝角,则$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$<0,由此列不等式,注意运用P满足双曲线的方程和双曲线的范围,即可解得P点横坐标的取值范围.
解答 解:双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{4}$=1的焦点为F1(-2$\sqrt{2}$,0),F2(2$\sqrt{2}$,0),
设P(x,y),
可得$\overrightarrow{P{F}_{1}}$=(-x-2$\sqrt{2}$,-y),$\overrightarrow{P{F}_{2}}$=(2$\sqrt{2}$-x,-y),
∵∠F1PF2为钝角,
∴$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$<0,
∴cos∠F1PF2<0,
∴(-x-2$\sqrt{2}$,-y)•(2$\sqrt{2}$-x,-y)<0,
即x2+y2-8<0,
又x2-y2=4,
∴y2=x2-4,即有x2<6,
解得-$\sqrt{6}$<x<$\sqrt{6}$,
又x>2或x<-2,
可得x∈(-$\sqrt{6}$,-2)∪(2,$\sqrt{6}$).
故答案为:(-$\sqrt{6}$,-2)∪(2,$\sqrt{6}$).
点评 本题考查双曲线的标准方程及向量知识,解题时要能熟练运用双曲线的方程和范围,考查运算能力,属于中档题.

练习册系列答案
相关题目
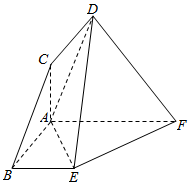 如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA=$\frac{π}{3}$,ABEF为直角梯形,BE∥AF,∠BAF=$\frac{π}{2}$,BE=2,AF=3,平面ABCD⊥平面ABEF.
如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA=$\frac{π}{3}$,ABEF为直角梯形,BE∥AF,∠BAF=$\frac{π}{2}$,BE=2,AF=3,平面ABCD⊥平面ABEF.