题目内容
8.数列{an}中,an+1=an+a(n∈N*,a为常数),若平面上三个不重合的点A,B,C共线,且该直线不过点O,且$\overrightarrow{OC}$=$\frac{{a}_{1}}{2}$$\overrightarrow{OA}$+$\frac{{a}_{2011}}{2}$$\overrightarrow{OB}$,则S2011等于( )| A. | 1005 | B. | $\frac{1}{2}$ | C. | 2010 | D. | 2011 |
分析 平面上三个不重合的点A,B,C共线,且该直线不过点O,且$\overrightarrow{OC}$=$\frac{{a}_{1}}{2}$$\overrightarrow{OA}$+$\frac{{a}_{2011}}{2}$$\overrightarrow{OB}$,l利用向量共线定理可得:$\frac{{a}_{1}}{2}$+$\frac{{a}_{2011}}{2}$=1.由于数列{an}中,an+1=an+a(n∈N*,a为常数),可得此数列是等差数列,即可得出.
解答 解:∵平面上三个不重合的点A,B,C共线,且该直线不过点O,且$\overrightarrow{OC}$=$\frac{{a}_{1}}{2}$$\overrightarrow{OA}$+$\frac{{a}_{2011}}{2}$$\overrightarrow{OB}$,
∴$\frac{{a}_{1}}{2}$+$\frac{{a}_{2011}}{2}$=1,
∵数列{an}中,an+1=an+a(n∈N*,a为常数),
∴此数列是等差数列,
则S2011=$\frac{2011({a}_{1}+{a}_{2011})}{2}$=2011,
故选:D.
点评 本题考查了向量共线定理、等差数列的通项公式性质及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.已知函数f(x)=xln(x-1)-a,下列说法正确的是( )
| A. | 当a>0时,f(x)有零点x0,且x0∈(1,2) | B. | 当a>0时,f(x)有零点x0,且x0∈(2,+∞) | ||
| C. | 当a=0时,f(x)没有零点 | D. | 当a<0时,f(x)有零点x0,且x0∈(2,+∞) |
19.已知z=$\frac{(1+2i)(3+4i)}{(2-i)^{3}}$,则|z|=( )
| A. | $\sqrt{5}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 1 |
16.在一个含有8个节目的节目单中,临时插入2个唱歌节目,且保持原节目顺序,则有( )种插入方法.
| A. | 90 | B. | 80 | C. | 72 | D. | 56 |
20.任取一个五位数,其能被5整除的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
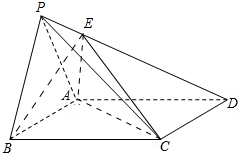 如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点E在棱PD上,且AE⊥PD
如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点E在棱PD上,且AE⊥PD