题目内容
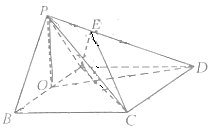 在四棱锥P-ABCD中,△PAB是边长为2的正三角形,底面ABCD为菱形,O为AB的中点,且PO⊥平面ABCD,OD与AC交于点F,E为PD上一点,且PD=3PE.
在四棱锥P-ABCD中,△PAB是边长为2的正三角形,底面ABCD为菱形,O为AB的中点,且PO⊥平面ABCD,OD与AC交于点F,E为PD上一点,且PD=3PE.(1)求证:平面ACE⊥平面ABCD;
(2)若∠ABC=60°,求异面直线AB与CE所成角的余弦值.
考点:异面直线及其所成的角,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)首先根据已知条件,通过成比例得到EF∥PO,另因为PO⊥平面ABCD,所以EF⊥平面ABCD.
,进一步求得结果.
(2)利用(1)的结论进一步把异面直线的夹角进行转化成CD与CE所成的角.进一步利用所求的线段长,利用余弦定理求出结果.
,进一步求得结果.
(2)利用(1)的结论进一步把异面直线的夹角进行转化成CD与CE所成的角.进一步利用所求的线段长,利用余弦定理求出结果.
解答:
证明:(1)连接EF,由于在平面ABCD中,AC和OD相交于F,
已知△PAB是边长为2的正三角形,底面ABCD为菱形,O为AB的中点,
根据平行线分线段成比例定理:
=
=
由于:PD=3PE.
则:
=
=
所以:EF∥PO,
PO⊥平面ABCD,
所以:EF⊥平面ABCD.
EF?平面ACE
所以:平面ACE⊥平面ABCD.
(2)在△AOD中,
已知:∠ABC=60°,
则:∠BAD=120°
进一步求出:OP=
,OD=2,OA=1
利用余弦定理:DO2=AO2+AD2-2AO•ADcos∠OAD
解得:DO=
由:△PAB是边长为2的正三角形
解得:PO=
所以:PD=
进一步解得:DE=
由题意得:AC=2,
根据比例的关系进一步求得:CF=
,EF=
,
利用EF⊥平面ABCD.
所以:CE2=EF2+CF2
解得:CE=
由于:AB∥CD,
则:异面直线AB与CE所成角即是CD与CE所成的角.
在△CED中,利用余弦定理:cos∠ECD=
解得:cos∠ECD=
所以:异面直线AB与CE所成角的余弦值为
.
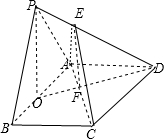
已知△PAB是边长为2的正三角形,底面ABCD为菱形,O为AB的中点,
根据平行线分线段成比例定理:
| DF |
| OF |
| CD |
| OA |
| 2 |
| 1 |
由于:PD=3PE.
则:
| OF |
| FD |
| PE |
| ED |
| 1 |
| 2 |
所以:EF∥PO,
PO⊥平面ABCD,
所以:EF⊥平面ABCD.
EF?平面ACE
所以:平面ACE⊥平面ABCD.
(2)在△AOD中,
已知:∠ABC=60°,
则:∠BAD=120°
进一步求出:OP=
| 3 |
利用余弦定理:DO2=AO2+AD2-2AO•ADcos∠OAD
解得:DO=
| 7 |
由:△PAB是边长为2的正三角形
解得:PO=
| 3 |
所以:PD=
| 10 |
进一步解得:DE=
2
| ||
| 3 |
由题意得:AC=2,
根据比例的关系进一步求得:CF=
| 4 |
| 3 |
2
| ||
| 3 |
利用EF⊥平面ABCD.
所以:CE2=EF2+CF2
解得:CE=
2
| ||
| 3 |
由于:AB∥CD,
则:异面直线AB与CE所成角即是CD与CE所成的角.
在△CED中,利用余弦定理:cos∠ECD=
| CE2+CD2-DE2 |
| 2CE•CD |
解得:cos∠ECD=
13
| ||
| 21 |
所以:异面直线AB与CE所成角的余弦值为
13
| ||
| 21 |

点评:本题考查的知识要点:线面垂直与面面垂直之间的转化,解三角形知识,勾股定理的应用,平行线分线段成比例定理,异面直线的夹角问题.属于基础题型.

练习册系列答案
相关题目
在不等式组
确定的平面区域中,若z=x+2y的最大值为6,则a的值为( )
|
| A、-2 | B、2 | C、-6 | D、6 |
函数f(x)=x2-2x-3的零点是( )
| A、x=-1和x=3 |
| B、x=-3和x=1 |
| C、(-1,0)和(3,0) |
| D、(-3,0)和(1,0) |
已知-
≤α<β≤
,则
的范围是( )
| π |
| 2 |
| π |
| 2 |
| α-β |
| 2 |
A、(-
| ||
B、[-
| ||
C、(-
| ||
D、[-
|
正整数集合Ak的最小元素为1,最大元素为2007,并且各元素可以从小到大排成一个公差为k的等差数列,则并集A17∪A59中的元素个数为( )
| A、119 | B、120 |
| C、151 | D、154 |
等比数列{an}的前n项和为Sn,且S3=14,a1=2,则a4=( )
| A、16 | B、16或-16 |
| C、-54 | D、16或-54 |
下列函数中与y=x相同的是( )
A、y=(
| |||
B、y=
| |||
C、y=
| |||
| D、y=|x| |
已知i为虚数单位,复数z满足i3•z=1-3i,则z=( )
| A、-3+i | B、-3-i |
| C、3+i | D、3-i |