题目内容
已知i为虚数单位,复数z满足i3•z=1-3i,则z=( )
| A、-3+i | B、-3-i |
| C、3+i | D、3-i |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:利用复数的运算法则即可得出.
解答:
解:∵复数z满足i3•z=1-3i,∴-i•z=1-3i,
∴z=
=
=3+i.
故选:C.
∴z=
| 1-3i |
| -i |
| (1-3i)i |
| -i•i |
故选:C.
点评:本题考查了复数的运算法则,属于基础题.

练习册系列答案
相关题目
2sin(-210°)的值为( )
A、-
| ||
| B、1 | ||
C、
| ||
| D、0 |
设复数z1=1-i,z2=2+i,其中i为虚数单位,则z1•z2的虚部为( )
| A、-1 | B、1 | C、-i | D、i |
若全集U={1,2,3,4,5,6},M={1,4},N={2,3},则集合(∁UM)∩N等于( )
| A、{2,3} |
| B、{2,3,5,6} |
| C、{1,4} |
| D、{1,4,5,6} |
若a2+b2=1,c2+d2=1,则下面的不等式中正确的是( )
A、abcd≤
| ||||
B、abcd≥
| ||||
C、0≤abcd≤
| ||||
D、-
|
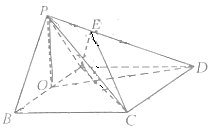 在四棱锥P-ABCD中,△PAB是边长为2的正三角形,底面ABCD为菱形,O为AB的中点,且PO⊥平面ABCD,OD与AC交于点F,E为PD上一点,且PD=3PE.
在四棱锥P-ABCD中,△PAB是边长为2的正三角形,底面ABCD为菱形,O为AB的中点,且PO⊥平面ABCD,OD与AC交于点F,E为PD上一点,且PD=3PE.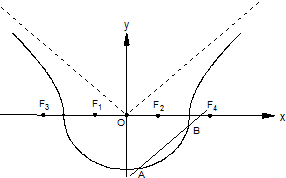 如图,曲线Γ由曲线C1:
如图,曲线Γ由曲线C1: