题目内容
函数f(x)=x2-2x-3的零点是( )
| A、x=-1和x=3 |
| B、x=-3和x=1 |
| C、(-1,0)和(3,0) |
| D、(-3,0)和(1,0) |
考点:函数的零点
专题:计算题,函数的性质及应用
分析:由题意,函数f(x)=x2-2x-3的零点即方程x2-2x-3=0的根,解方程即可.
解答:
解:函数f(x)=x2-2x-3的零点即
方程x2-2x-3=0的根,
解方程可得,x=3或x=-1;
故选A.
方程x2-2x-3=0的根,
解方程可得,x=3或x=-1;
故选A.
点评:本题考查了函数的零点与方程的根的关系应用,属于基础题.

练习册系列答案
相关题目
已知函数f(x)是定义在区间[3a-5,2a]上的奇函数,则实数a的值为( )
| A、1 | ||
B、
| ||
| C、0 | ||
| D、不确定 |
“双曲线C的渐近线方程为y=±
x”是“双曲线C的方程为
-
=1”的( )
| 4 |
| 3 |
| x2 |
| 9 |
| y2 |
| 16 |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、不充分不必要条件 |
设等差数列{an}的前n项和为Sn,若a1=-11,a4+a6=-6,S5等于( )
| A、-35 | B、-30 |
| C、30 | D、20 |
设复数z1=1-i,z2=2+i,其中i为虚数单位,则z1•z2的虚部为( )
| A、-1 | B、1 | C、-i | D、i |
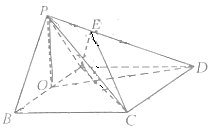 在四棱锥P-ABCD中,△PAB是边长为2的正三角形,底面ABCD为菱形,O为AB的中点,且PO⊥平面ABCD,OD与AC交于点F,E为PD上一点,且PD=3PE.
在四棱锥P-ABCD中,△PAB是边长为2的正三角形,底面ABCD为菱形,O为AB的中点,且PO⊥平面ABCD,OD与AC交于点F,E为PD上一点,且PD=3PE.