题目内容
某校高一、高二、高三分别有3、2、1人获得校演讲比赛优胜奖,学校决定在这6名获奖学生中随机抽取2名学生进行培训参加县里演讲比赛,则高二至少有一名学生参加县里测试的概率为 .
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:设高一的3位同学为A1,A2,A3,高二的2位同学为B1,B2,高三的1位同学为C1,列举可得总的基本事件有15个,符合条件的有9个,由概率公式可得.
解答:
解:设高一的3位同学为A1,A2,A3,高二的2位同学为B1,B2,高三的1位同学为C1,
则从六位同学中抽两位同学有15种可能,列举如下:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),
(A1,C1),(A2,A3),(A2,B1),(A2,B2),
(A2,C1),(A3,B1),(A3,B2),(A3,C1),
(B1,B2),(B1,C1),(B2,C1),
其中高二的2位同学至少一位同学参加县里测试的有:
(A1,B1),(A1,B2),(A2,B1),(A2,B2),
(A3,B1),(B1,B2),(A3,B2),(B1,C1),(B2,C1)9种可能.
∴高二至少有一名学生参加县里比赛的概率为:
=
故答案为:
则从六位同学中抽两位同学有15种可能,列举如下:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),
(A1,C1),(A2,A3),(A2,B1),(A2,B2),
(A2,C1),(A3,B1),(A3,B2),(A3,C1),
(B1,B2),(B1,C1),(B2,C1),
其中高二的2位同学至少一位同学参加县里测试的有:
(A1,B1),(A1,B2),(A2,B1),(A2,B2),
(A3,B1),(B1,B2),(A3,B2),(B1,C1),(B2,C1)9种可能.
∴高二至少有一名学生参加县里比赛的概率为:
| 9 |
| 15 |
| 3 |
| 5 |
故答案为:
| 3 |
| 5 |
点评:本题考查列举法计算基本事件数及事件发生的概率,属基础题.

练习册系列答案
相关题目
已知函数f(x)是定义在区间[3a-5,2a]上的奇函数,则实数a的值为( )
| A、1 | ||
B、
| ||
| C、0 | ||
| D、不确定 |
如果命题p∨q为真命题,p∧q为假命题,那么( )
| A、命题p、q都是真命题 |
| B、命题p、q都是假命题 |
| C、命题p、q至少有一个是真命题 |
| D、命题p、q只有一个真命题 |
若a、b是任意实数,且a>b,则下列不等式恒成立的是( )
| A、a2>b2 | ||||
B、
| ||||
| C、lg(a-b)>0 | ||||
D、(
|
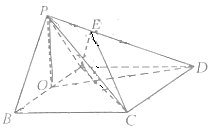 在四棱锥P-ABCD中,△PAB是边长为2的正三角形,底面ABCD为菱形,O为AB的中点,且PO⊥平面ABCD,OD与AC交于点F,E为PD上一点,且PD=3PE.
在四棱锥P-ABCD中,△PAB是边长为2的正三角形,底面ABCD为菱形,O为AB的中点,且PO⊥平面ABCD,OD与AC交于点F,E为PD上一点,且PD=3PE.