题目内容
已知f(x)=cos 2x-1,g(x)=f(x+m)+n,则使g(x)为奇函数的实数m,n的可能取值为( )
A、m=
| ||
B、m=
| ||
C、m=-
| ||
D、m=-
|
考点:函数奇偶性的性质,函数奇偶性的判断
专题:函数的性质及应用
分析:g(x)=f(x+m)+n=cos(2x+2m)-1+n,由于g(x)为奇函数,可得2m=kπ+
,(k∈Z),-1+n=0.
| π |
| 2 |
解答:
解:g(x)=f(x+m)+n=cos(2x+2m)-1+n,
∵g(x)为奇函数,∴2m=kπ+
,(k∈Z),-1+n=0.
当k=0时,解得m=-
,n=1.
故选:D.
∵g(x)为奇函数,∴2m=kπ+
| π |
| 2 |
当k=0时,解得m=-
| π |
| 4 |
故选:D.
点评:本题考查了三角函数的奇偶性,考查了推理能力,属于基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
设a=40.1,b=log40.1,c=0.40.1,则( )
| A、a>b>c |
| B、b>a>c |
| C、a>c>b |
| D、b>c>a |
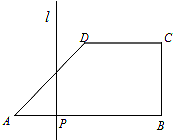 在直角梯形ABCD中,AB∥DC,AB⊥BC,且AB=4,BC=CD=2,点P为线段AB上的一动点,过点P作直线l⊥AB,令AP=x,记梯形位于直线l左侧部分的面积S=f(x).
在直角梯形ABCD中,AB∥DC,AB⊥BC,且AB=4,BC=CD=2,点P为线段AB上的一动点,过点P作直线l⊥AB,令AP=x,记梯形位于直线l左侧部分的面积S=f(x).