题目内容
已知实数x,y满足
,则x2+y2的取值范围是( )
|
A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,设z=x2+y2,利用z的几何意义即可得到结论.
解答:
解:作出不等式组对应的平面区域如图(阴影部分):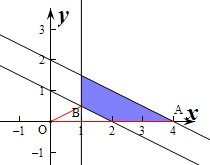
设z=x2+y2,则z的几何意义为阴影部分的点P(x,y)到原点距离的平方,
由图象知:当P位于点B(1,
)时,此时|OB|的距离最小,
当P位于点A(4,0)时,|OA|的距离最大,
即|0B|=
=
,|0A|=4,
∴|OB|2≤z≤|OA|2,
即
≤z≤16,
∴x2+y2的取值范围是[
,16],
故选:B

设z=x2+y2,则z的几何意义为阴影部分的点P(x,y)到原点距离的平方,
由图象知:当P位于点B(1,
| 1 |
| 2 |
当P位于点A(4,0)时,|OA|的距离最大,
即|0B|=
12+(
|
|
∴|OB|2≤z≤|OA|2,
即
| 5 |
| 4 |
∴x2+y2的取值范围是[
| 5 |
| 4 |
故选:B
点评:本题主要考查线性规划、点到直线的距离公式的应用,利用数形结合是解决本题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
已知三条不重合的直线m,n,l和两个不重合的平面α、β,下列命题中正确命题个数为( )
①若m∥n,n?α,则m∥α;②若l⊥α,m⊥β且l⊥m则α⊥β
③若l⊥n,m⊥n,则l∥m④若α⊥β,α∩β=m,n?β,n⊥m,则n⊥α
①若m∥n,n?α,则m∥α;②若l⊥α,m⊥β且l⊥m则α⊥β
③若l⊥n,m⊥n,则l∥m④若α⊥β,α∩β=m,n?β,n⊥m,则n⊥α
| A、1 | B、2 | C、3 | D、4 |
过双曲线
-
=1(a>0,b>0)的一个焦点作实轴的垂线,交双曲线于A,B两点,若线段AB的长度恰等于焦距,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在下列四个命题中
①y=1是幂函数;
②“x<1”是“x<2”的充分不必要条件;
③命题“存在x∈R,x2-2>0”的否定是:“任意x∈R,x2-x<0”
④若a=-1,则函数f(x)=ax2+2x-1只有一个零点.
其中错误的个数有( )个.
①y=1是幂函数;
②“x<1”是“x<2”的充分不必要条件;
③命题“存在x∈R,x2-2>0”的否定是:“任意x∈R,x2-x<0”
④若a=-1,则函数f(x)=ax2+2x-1只有一个零点.
其中错误的个数有( )个.
| A、4 | B、2 | C、3 | D、1 |
已知变量x,y满足约束条件
,则z=4x+y的最小值为( )
|
| A、55 | B、-55 | C、5 | D、-5 |
已知集合A={x||2x+1|>3},集合B={x|y=
},则A∩(∁RB)=( )
|
| A、(1,2) |
| B、(1,2] |
| C、(1,+∞) |
| D、[1,2] |
 某商家推出一款简单电子游戏,弹射一次可以将三个相同的小球随机弹到一个正六边形的顶点与中心共七个点中的三个位置上(如图),用S表示这三个球为顶点的三角形的面积.规定:当三球共线时,S=0;当S最大时,中一等奖,当S最小时,中二等奖,其余情况不中奖,一次游戏只能弹射一次.
某商家推出一款简单电子游戏,弹射一次可以将三个相同的小球随机弹到一个正六边形的顶点与中心共七个点中的三个位置上(如图),用S表示这三个球为顶点的三角形的面积.规定:当三球共线时,S=0;当S最大时,中一等奖,当S最小时,中二等奖,其余情况不中奖,一次游戏只能弹射一次.