题目内容
设Sn是公差不为0的等差数列{an}的前n项和，S3=9，且S1，S2，S4成等比数列，则a7的值为（ ）
| A、7 | B、11 | C、13 | D、22 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：由题意S1，S2，S4成等比数列，即S22=S1•S4，化简可得d=2a1，结合S3=9，求出a1=1，d=2，即可求出a7的值．
解答：
解：数列{an}是公差不为0的等差数列，设公差为d，
∵S1，S2，S4成等比数列，∴S22=S1•S4，
∴（ 2a1+d）2=a1•（4a1+6d），化简可得d=2a1，
∵S3=9，
∴3a1+3d=9，
∴a1=1，d=2，
∴a7=a1+6d=13．
故选：C．
∵S1，S2，S4成等比数列，∴S22=S1•S4，
∴（ 2a1+d）2=a1•（4a1+6d），化简可得d=2a1，
∵S3=9，
∴3a1+3d=9，
∴a1=1，d=2，
∴a7=a1+6d=13．
故选：C．
点评：本题考查等比数列的性质，考查等差数列的通项与求和，确定a1=1，d=2是关键．
练习册系列答案
相关题目
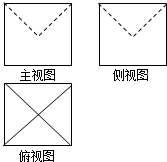某几何体的三视图如图所示，图中的四边形都是边长为1的正方形，两条虚线互相垂直，则该几何体的体积是（ ）A、
| ||
B、
| ||
C、
| ||
| D、1 |
已知复数z1=（2-i）i，复数z2=a+3i（a∈R），若复数z2=kz1（k∈R），则a=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，在△ABC中，∠C=90°，CA=CB=1，P为△ABC内一点，过点P分别引三边的平行线，与各边围成以P为顶点的三个三角形（图中阴影部分），则这三个三角形的面积和的最小值为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
已知直线x=
和点（
，0）恰好是函数f（x）=
sin（ωx+φ）图象的相邻的对称轴和对称中心，则f（x）的表达式可以是（ ）
| 5π |
| 12 |
| π |
| 6 |
| 2 |
A、f（x）=
| ||||
B、f（x）=
| ||||
C、f（x）=
| ||||
D、f（x）=
|