Question

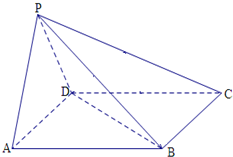如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，△PAD是边长为2的正三角形，四边形ABCD为菱形，且∠DAB=60°，PC=

10

（1）求PC与面ABCD所成角的正弦值；
（2）求二面角P-BC-A的平面角的大小；
（3）平面PBC与平面PAD交于直线l，画出直线l，并判断直线l与直线BC的关系．

Answer 1

考点：与二面角有关的立体几何综合题,直线与平面所成的角

专题：空间角

分析：（1）以D为原点，DA为x轴，过点D垂直BC的直线为y轴，过点D垂直于平面ABCD的直线为z轴，建立空间直角坐标系，利用向量法能求出PC与面ABCD所成角的正弦值．
（2）分别求出平面PBC的法向量和平面BCA的法向量，利用向量法能求出二面角P-BC-A的平面角的大小．
（3）过点A作AQ∥DP，过P作PQ∥AD，交AQ于点Q，直线PQ就是直线l，由此能判断l∥BC．

解答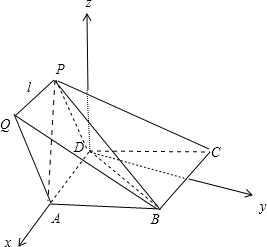： 解：（1）如图，∵在四棱锥P-ABCD中，
平面PAD⊥平面ABCD，△PAD是边长为2的正三角形，
四边形ABCD为菱形，且∠DAB=60°，PC=

10

，
∴以D为原点，DA为x轴，过点D垂直BC的直线为y轴，
过点D垂直于平面ABCD的直线为z轴，
建立空间直角坐标系，
则P（1，0，

3

），C（-1，

3

，0），
∴

PC

=（-2，

3

，-

3

），B（1，

3

，0），
面ABCD的法向量

n

=（0，0，1），
设PC与平面ABCD所成的角为θ，
则sinθ=|cos＜

PC

，

n

＞|=|

- 3

10

|=

30

10

，
∴PC与面ABCD所成角的正弦值为

30

10

．
（2）

PB

=(0，

3

，-

3

)

PC

=(-2，

3

，-

3

)，
设平面PBC的法向量

m

=（x，y，z），
则

m • PB = 3 y- 3 z=0 m • PC =-2x+ 3 y- 3 z=0

，
取y=1，得

m

=（0，1，1），
平面BCA的法向量

n

=（0，0，1），
∴cos＜

m

，

n

＞=

1

2

=

2

2

∴二面角P-BC-A的平面角的大小为45°．
（3）过点A作AQ∥DP，过P作PQ∥AD，交AQ于点Q，连结BQ，
∵PQ∥AD，∴ADPQ是平面，
∵PQ∥AD，AD∥BC，∴PQ∥BC，
∴BCPQ也是一个平面，
∴平面ADPQ∩平面BCPQ=PQ，
∵平面PBC与平面PAD交于直线l，∴直线PQ就是直线l，
∵l∥AD，BC∥AD，
∴l∥BC．
故直线l与直线BC平行．

点评：本题考查空间点、线、面位置关系，考查二面角、空间向量及坐标运算等基础知识，考查空间想象能力、运算能力和推理论能力，考查用向量方法解决问题能力．