题目内容
(文)已知点D(1,
)在双曲线C:
-
=1(a>0,b>0)上,且双曲线的一条渐近线的方程是
x+y=0.
(1)求双曲线C的方程;
(2)若过点(0,1)且斜率为k的直线l与双曲线C有两个不同交点,求实数k的取值范围;
(3)设(2)中直线l与双曲线C交于A、B两个不同点,若以线段AB为直径的圆经过坐标原点,求实数k的值.
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(1)求双曲线C的方程;
(2)若过点(0,1)且斜率为k的直线l与双曲线C有两个不同交点,求实数k的取值范围;
(3)设(2)中直线l与双曲线C交于A、B两个不同点,若以线段AB为直径的圆经过坐标原点,求实数k的值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)点D(1,
)代入双曲线方程,结合且双曲线的一条渐近线的方程是
x+y=0,建立方程,求出a,b,即可求双曲线C的方程;
(2)直接联立直线与双曲线方程,化为关于x的一元二次方程,利用根的判别式,即可求实数k的取值范围;
(3)存在实数k,使得以线段AB为直径的圆经过坐标原点转化为kOA•kOB=-1,即x1x2+y1y2=0,整理后代入根与系数关系求解实数k的值.
| 2 |
| 3 |
(2)直接联立直线与双曲线方程,化为关于x的一元二次方程,利用根的判别式,即可求实数k的取值范围;
(3)存在实数k,使得以线段AB为直径的圆经过坐标原点转化为kOA•kOB=-1,即x1x2+y1y2=0,整理后代入根与系数关系求解实数k的值.
解答:
解:(1)由题知,有
解得a2=
,b2=1
因此,所求双曲线C的方程是
-y2=1
(2)∵直线l过点(0,1)且斜率为k,
∴直线l:y=kx+1.
代入双曲线方程得(3-k2)x2-2kx-2=0.
又直线l与双曲线C有两个不同交点,
∴3-k2≠0且△=(-2k)2+8(3-k2)>0
解得k∈(-
,-
)∪(-
,
)∪(
,
).
(3)设点A、B的坐标为(x1,y1)、(x2,y2).
由(2)可得x1+x2=
,x1x2=
又以线段AB为直径的圆经过坐标原点,
则kOA•kOB=-1,即x1x2+y1y2=0,
∴x1x2+(kx1+1)(kx2+1)=0,
即(k2+1)x1x2+k(x1+x2)+1=0,
∴
+
+1=0,解得k=±1.
又k=±1满足3-k2≠0且△=(-2k)2+8(3-k2)>0,
∴所求实数k=±1.
|
解得a2=
| 1 |
| 3 |
因此,所求双曲线C的方程是
| x2 | ||
|
(2)∵直线l过点(0,1)且斜率为k,
∴直线l:y=kx+1.
代入双曲线方程得(3-k2)x2-2kx-2=0.
又直线l与双曲线C有两个不同交点,
∴3-k2≠0且△=(-2k)2+8(3-k2)>0
解得k∈(-
| 6 |
| 3 |
| 3 |
| 3 |
| 3 |
| 6 |
(3)设点A、B的坐标为(x1,y1)、(x2,y2).
由(2)可得x1+x2=
| 2k |
| 3-k2 |
| -2 |
| 3-k2 |
又以线段AB为直径的圆经过坐标原点,
则kOA•kOB=-1,即x1x2+y1y2=0,
∴x1x2+(kx1+1)(kx2+1)=0,
即(k2+1)x1x2+k(x1+x2)+1=0,
∴
| -2(1+k2) |
| 3-k2 |
| 2k2 |
| 3-k2 |
又k=±1满足3-k2≠0且△=(-2k)2+8(3-k2)>0,
∴所求实数k=±1.
点评:本题主要考查了直线与双曲线的位置关系的应用,直线与曲线联立,根据方程的根与系数的关系解题,是处理这类问题的最为常用的方法,训练了利用直线斜率的关系判断两直线的垂直关系,是中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
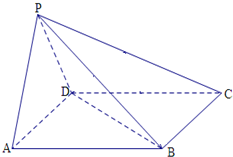 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是边长为2的正三角形,四边形ABCD为菱形,且∠DAB=60°,PC=
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是边长为2的正三角形,四边形ABCD为菱形,且∠DAB=60°,PC=