题目内容
求数集{a，a2-a}中实数a的取值范围．
考点：集合的确定性、互异性、无序性,元素与集合关系的判断
专题：集合
分析：根据元素的互异性即可得到结论．
解答：
解：根据集合元素的互异性可知：a2-a≠a，即a2≠2a，
∴a≠0且a≠2，
故实数a的取值范围是{a|a≠0且a≠2}．
∴a≠0且a≠2，
故实数a的取值范围是{a|a≠0且a≠2}．
点评：本题主要考查集合元素的性质，利用集合元素的互异性是解决本题的关键，比较基础．
练习册系列答案
智能训练练测考系列答案
相关题目
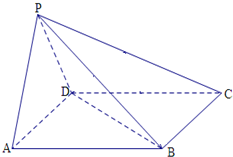如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，△PAD是边长为2的正三角形，四边形ABCD为菱形，且∠DAB=60°，PC=