题目内容
某工厂生产A,B两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
由于表格被污损,数据x,y看不清,统计员只记得x<y,且A,B两种元件的检测数据的平均值相等,方差也相等.
(Ⅰ)表格中x+y=
(Ⅱ)从被检测的5件B种元件中任取2件,2件都为正品的概率为 .
| A | 7 | 7 | 7.5 | 9 | 9.5 |
| B | 6 | x | 8.5 | 8.5 | y |
(Ⅰ)表格中x+y=
(Ⅱ)从被检测的5件B种元件中任取2件,2件都为正品的概率为
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)由已知中A,B两种元件的检测数据的平均值相等,方差也相等,可得x+y=17且(x-8)2+(y-8)2=1,结合x<y,可求出表格中x与y的值;
(Ⅱ)从被检测的5件B种元件中任取2件,共有
=10种不同的情况,记“抽取2件都为正品”为事件A,则事件A共包含
=6种不同的情况,进而可求得结果.
(Ⅱ)从被检测的5件B种元件中任取2件,共有
| C | 2 5 |
| C | 2 4 |
解答:
解:(Ⅰ)∵
=
(7+7+7.5+9+9.5)=8,
=
(6+x+8.5+8.5+y),
∵
=
,
∴x+y=17…①
∵SA2=
(1+1+0.25+1+2.25)=1.1,SB2=
[4+(x-8)2+0.25+0.25+(y-8)2],
∵SA2=SB2,
∴(x-8)2+(y-8)2=1…②
由①②结合x<y得:x=8,y=9.
(Ⅱ)记被检测的5件B种元件为:A,B,C,D,E,其中A,B,C,D为正品,从中选取的两件为(x,y)
则共有
=10种不同的情况,分别为:
(A,B),(A,C),(A,D),(A,E),(B,C),
(B,D),(B,E),(C,D),(C,E),(D,E),
记“抽取2件都为正品”为事件A,
则事件A共包含
=6种不同的情况,分别为:
(A,B),(A,C),(A,D),(B,C),(B,D),(C,D),
故P(A)=
=
,
即2件都为正品的概率为:
.
. |
| xA |
| 1 |
| 5 |
. |
| xB |
| 1 |
| 5 |
∵
. |
| xA |
. |
| xB |
∴x+y=17…①
∵SA2=
| 1 |
| 5 |
| 1 |
| 5 |
∵SA2=SB2,
∴(x-8)2+(y-8)2=1…②
由①②结合x<y得:x=8,y=9.
(Ⅱ)记被检测的5件B种元件为:A,B,C,D,E,其中A,B,C,D为正品,从中选取的两件为(x,y)
则共有
| C | 2 5 |
(A,B),(A,C),(A,D),(A,E),(B,C),
(B,D),(B,E),(C,D),(C,E),(D,E),
记“抽取2件都为正品”为事件A,
则事件A共包含
| C | 2 4 |
(A,B),(A,C),(A,D),(B,C),(B,D),(C,D),
故P(A)=
| 6 |
| 10 |
| 3 |
| 5 |
即2件都为正品的概率为:
| 3 |
| 5 |
| 3 |
| 5 |
点评:本题考查的知识点是古典概型及其概率计算公式,平均数与方差,是统计与概率的综合应用,但难度不大,属于基础题.

练习册系列答案
相关题目
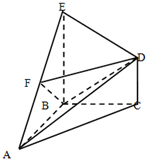 如图,在几何体ABCDE中,BE⊥平面ABC,CD∥BE,△ABC是等腰直角三角形,∠ABC=90°,且BE=AB=2,CD=1,点F是AE的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题:
如图,在几何体ABCDE中,BE⊥平面ABC,CD∥BE,△ABC是等腰直角三角形,∠ABC=90°,且BE=AB=2,CD=1,点F是AE的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题: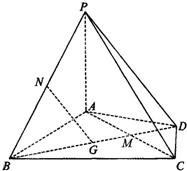 在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥AB,△ABC是正三角形,AC与BD的交点M恰好是AC中点,N为线段PB的中点,G在线段BM上,且
在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥AB,△ABC是正三角形,AC与BD的交点M恰好是AC中点,N为线段PB的中点,G在线段BM上,且 在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E为BB1中点.
在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E为BB1中点.