题目内容
若函数f(x)=2lnx+x2-5x+c在区间(m,m+1)上为递减函数,则m的取值范围是 .
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:先求出函数f(x)的导数,由题意得出方程组,解出即可.
解答:
解:∵函数f(x)=2lnx+x2-5x+c,
∴f′(x)=
+2x-5,
又函数f(x)在区间(m,m+1)上为递减函数,
∴
,
解得:
≤m≤1,
故答案为:[
,1].
∴f′(x)=
| 2 |
| x |
又函数f(x)在区间(m,m+1)上为递减函数,
∴
|
解得:
| 1 |
| 2 |
故答案为:[
| 1 |
| 2 |
点评:本题考察了函数的单调性问题,导数的应用问题,以及解方程组,本题是一道基础题.

练习册系列答案
相关题目
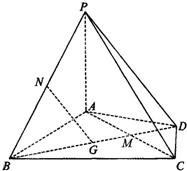 在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥AB,△ABC是正三角形,AC与BD的交点M恰好是AC中点,N为线段PB的中点,G在线段BM上,且
在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥AB,△ABC是正三角形,AC与BD的交点M恰好是AC中点,N为线段PB的中点,G在线段BM上,且 对一根作直线运动的质点的运动过程观测了8次,得到如下表所示的数据.
对一根作直线运动的质点的运动过程观测了8次,得到如下表所示的数据.