某几何体的三视图如图所示.则该几何体的体积为( )A．4B．5C．6D．7 题目和参考答案——青夏教育精英家教网—

题目内容

13．某几何体的三视图如图所示，则该几何体的体积为（　　）

A．

B．

C．

D．

分析根据三视图，可知元几何体是一个棱长分别为2、2、1的长方体和一个横放的直三棱柱的组合体，三棱柱底面是一个直角边分别为1、1的直角三角形，高是2，即可求出几何体体积．

解答解：根据三视图，可知元几何体是一个棱长分别为2、2、1的长方体和一个横放的直三棱柱的组合体，三棱柱底面是一个直角边分别为1、1的直角三角形，高是2，所以几何体体积是$V=2×2×1+\frac{1}{2}×1×1×2=5$．
故选B．

点评本题考查了由三视图求几何体的体积，解题的关键是判断几何体的形状及数据所对应的几何量．

练习册系列答案

4．已知椭圆$M：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率是$\frac{{\sqrt{2}}}{2}$，上顶点B是抛物线x²=4y的焦点．
（Ⅰ）求椭圆M的标准方程；
（Ⅱ）若P、Q是椭圆M上的两个动点，且OP⊥OQ（O是坐标原点），由点O作OR⊥PQ于R，试求点R的轨迹方程．

1．

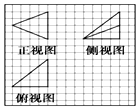如图，方格纸上正方形小格的边长为1，图中粗实线画出的是由一个正方体截得的一个几何体的三视图，则该几何体的体积为（　　）

8．小李参加一种红包接龙游戏：他在红包里塞了12元，然后发给朋友A，如果A猜中，A将获得红包里的所有金额；如果A未猜中，A将当前的红包转发给朋友B，如果B猜中，A、B平分红包里的金额；如果B未猜中，B将当前的红包转发给朋友C，如果C猜中，A、B和C平分红包里的金额；如果C未猜中，红包里的钱将退回小李的账户，设A、B、C猜中的概率分别为$\frac{1}{3}$，$\frac{1}{2}$，$\frac{1}{3}$，且A、B、C是否猜中互不影响．
（Ⅰ）求A恰好获得4元的概率；
（Ⅱ）设A获得的金额为X元，求X的分布列及X的数学期望．

18．已知曲线C的极坐标方程是ρ-2cosθ-4sinθ=0，以极点为在平面直角坐标系的原点，极轴为x轴的正半轴建立平面直角坐标系xoy，直线的参数方程为$\left\{\begin{array}{l}x=\frac{{\sqrt{3}}}{2}t\\ y=1+\frac{1}{2}t\end{array}\right.$（t为参数）．
（1）将曲线C的极坐标方程化为直角坐标方程，将直线l的参数方程化为普通方程；
（2）若直线l与曲线C相交于A，B两点，与y轴交于点M，求（|MA|+|MB|）²的值．

5．某几何体的三视图如图所示，则此几何体的体积为（　　）

2．在极坐标系中，以下是圆ρ=2cosθ的一条切线的是（　　）

3．

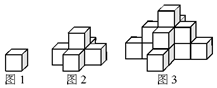图1是一个水平摆放的小正方体木块，图2，图3是由这样的小正方体木块叠放而成的，按照这样的规律放下去，至第六个叠放的图形中，小正方体木块总数就是（　　）

试题分类